剛性比例型減衰には初期剛性比例型減衰の他に、瞬間剛性比例型減衰と呼ばれるものがあります。
式で表現すると下式のように表されます。
この式では、構造物の剛性が低下した場合には粘性減衰も剛性に比例して低下させており、結果的に大きな応答値を導くことにより、安全側の設計を行うという考え方が根底にあると考えられます。
ここで、この式には以下のように4種類の解釈が考えられます。
・h1一定 累積型
・h1一定 非累積型
・α1一定 累積型
・α1一定 非累積型
「累積型」や「非累積型」は剛性変更時の減衰力の考え方、「h1一定」や「α1一定」は剛性変更時の減衰係数の大きさの考え方を意味しています。
では、それぞれの解釈の違いによる特徴を整理したいと思います。
【累積型と非累積型】
累積型は瞬間減衰係数と増分速度の積を累積したものをそのステップの減衰力とし、非累積型は瞬間減衰係数とそのステップの速度の積をそのステップの減衰力とします。
数式で表すと以下のようになります。
累積型: \(F_{(t)}=\Sigma(C_{(t)}\Delta V_{(t)})\) 非累積型: \(F_{(t)}=C_{(t)}(\Sigma\Delta V)=C_{(t)}V_{(t)}\)
F(t):時刻tの減衰力
C(t):時刻tの減衰係数
V(t):時刻tの速度
ΔV(t):増分速度 \(V_{(t)}-V_{(t-1)}\)
t:時刻
それぞれの特徴は以下の通りです。
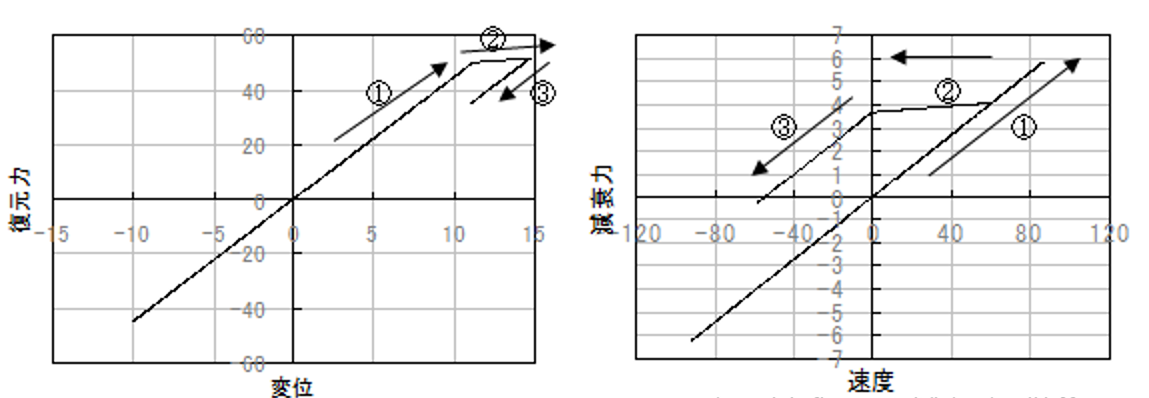
累積型の特徴:
・減衰力-速度関係が連続する
・残留変位が発生しやすい(原点を通過しない)
【数式的解釈】
・初期剛性時
\(F=C_1\Delta V_1+C_1\Delta V_2+...+C_1\Delta V_n\)
・剛性変更後
\(F=C_1\Delta V_1+C_1\Delta V_2+...+C_1\Delta V_n+C_2\Delta V_{n+1}+C_2\Delta V_{n+2}+...\)
C1:初期剛性に対する減衰係数
C2:剛性変更後の減衰係数
⇒ 剛性変更後も減衰力は連続的。
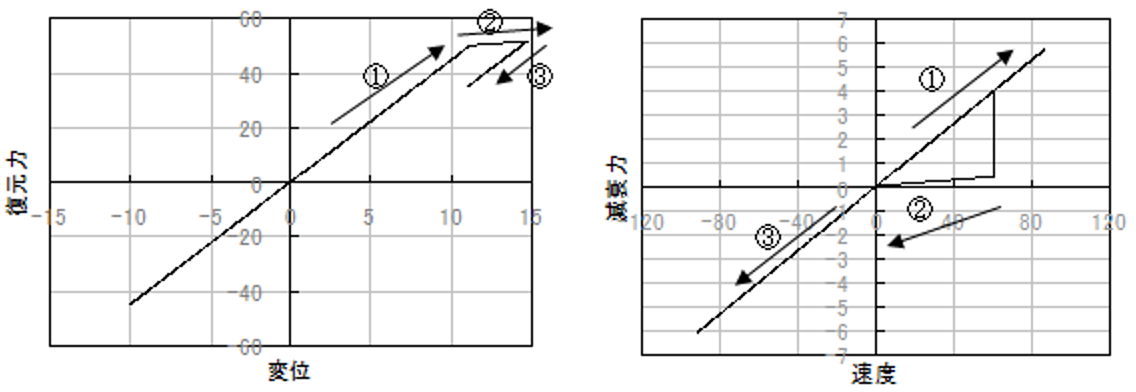
非累積型の特徴:
・減衰力-速度関係が不連続
・剛性変更時に減衰力が大きく変化して、瞬間的に大きな加速度を生じることがある
【数式的解釈】
・初期剛性時
\(F=C_1(\Delta V_1+\Delta V_2+...+\Delta V_n)\)
・剛性変更後
\(F=C_2(\Delta V_1+\Delta V_2+...+\Delta V_n+\Delta V_{n+1}+\Delta V_{n+2}+...)\)
C1:初期剛性に対する減衰係数
C2:剛性変更後の減衰係数
⇒ 剛性変更後に減衰力が大きく変わる可能性がある。

【α1一定とh1一定】
減衰係数の評価時に剛性に乗じる係数をどのように扱うかに違いがあります。
α1一定は剛性に乗じる係数α1を剛性変更による固有周期の変化に関わらず一定とします。
h1一定は剛性に乗じる係数α1を剛性変更による固有周期の変化に応じて変化させます。
α1一定の特徴:
・h1一定と比較して減衰を小さく評価する傾向にある
\([C]=\alpha _1[S]\), \(\alpha _1=2h_1/\omega\)指定した減衰定数h1と固有周期T1(ω1=2π/T1)からα1を求めて、
これを瞬間剛性に乗じて時々刻々の減衰力を計算します。
このα1については剛性変更が生じても一定とします。
h1一定の特徴:
・α1一定と比較して減衰を大きく評価する傾向にある
\([C]=\alpha _1[S]\), \(\alpha _1=2h_1/\omega\) \(\omega=\omega _1 \sqrt{\frac{\{u\}^T[S]\{u\}}{\{u\}^T[S_1]\{u\}}}\)ω1:初期剛性1次モードの円振動数 {u} 1次固有ベクトル [S1]:初期剛性マトリクス
「α1一定」と同様に、減衰定数h1に関しては指定された値を使用しますが、ωについては瞬間剛性を考慮して求めたものを使用するため剛性項に乗じる係数αについても塑性化による建物周期の伸びを考慮した計算となります。このため、「α1一定」と比較して減衰が大きくなる傾向にあります。
注意点
・h1一定の場合、初期剛性マトリクスを用いるため部材の「固有値解析にのみ用いられる」とされているばね剛性が減衰に影響を及ぼします。
・h1一定の場合、負剛性となる部材(NewRCモデルや若林モデルなど)があるモデルでは過大な変形が生じると瞬間剛性[S]が負の値となり、ωの計算における平方根の中身が負の値となり、正常に計算できない場合があります。
・基礎免震構造では一般的に免震層固定時の1次固有周期に対して減衰定数を決めて上部構造に減衰を与えます。h1一定の場合、免震層の剛性変更によりこの減衰が変更されてしまいます。 免震層の剛性変更が上部構造の減衰評価に寄与することは適切とは言い難く、この場合はα1一定の方が適切であると言えます。
まとめ
本日は、瞬間剛性比例型減衰の種類について整理してみました。
私たちは他の減衰タイプも含めて、解析目的や条件によって適切な減衰を選択する必要があります。
そのためにはまずそれぞれの減衰の考え方や特徴を把握しておく必要があると考えます。
参考文献:梁川幸盛ほか「地震応答解析における瞬間剛性比例型減衰についての考察」、日本建築学会大会学術講演梗概集、2004
