見たことある設定だけど・・・
解析ソフトを使って固有値解析をしていて、「出力するモード次数」などの文言を見たことはありますでしょうか。恐らく、多くの場合はこの部分の設定を変えずにデフォルト値で設定して、立体解析で有効質量比の大きいモードが出てない時などに初めて設定を変更するような値かと思われます。RESP-Dではモード別減衰を使うときなどにも変更した方がよいです。そもそも、何故この設定が必要かご存じでしょうか。今回は固有値解析のプログラムを作るにあたって考慮すべきことを記載してみます。
固有値解析のアルゴリズムについて
固有モードは解析モデルの全自由度の数だけ存在します。例えば、大規模なモデルで全自由度が20000ある場合は20000個の固有モードが存在します。しかし、これらの全てのモードが必要なわけではなく、影響の大きいモードが把握できれば問題がないので一部だけ求めるのが一般的です。一部と言っても影響の大きいモードをピンポイントで選ぶことはできないので、求める次数nを指定して固有値が大きい方からn個、もしくは、小さい方からn個に求めるようになります。建築構造物では固有周期が長い方に影響が大きいモードがあることが多いので、周期が長い(振動数が低い)モードの方からn個だけ求めていきます。RESP-Dでも以下の指定があります。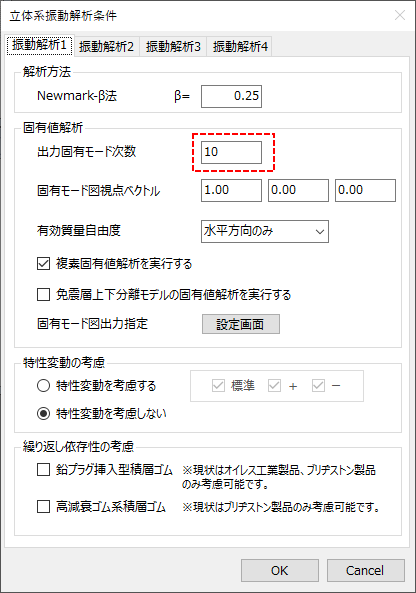
大規模なモデルに対して固有値が大きい、もしくは小さい順に求めるアルゴリズムとしてよく使われるのがサブスペース法やランチョス法です。ざっくりなイメージとしては大規模な行列を小さい行列に変換して、小さい行列の固有値を求めて計算負荷を軽減する方法です。
RESP-Dでは全自由度が3000以上の場合に大規模なモデルと判断してサブスペース法を適用します。
細かい話をすると、サブスペース法では求める次数を10にした場合でもプログラム内部では10+α個の固有値を求めていることが多いです。理由としてn次モードまで求めるとした時のn次固有ベクトルの収束率があまりよくない場合があるためです。
実際にプログラムを組んでみると、求める次数を10に設定した時に10次の固有ベクトルは反復計算がかなり進んだ段階でも収束しきっていなかったりします。
一般化固有値問題を標準固有値問題へ変換する
振動解析の時に行っている固有値解析は一般化固有値問題と呼ばれる次の式ものです。$$ Ax = \lambda B x $$
ここでA、Bは剛性マトリクス、もしくは、質量マトリクスのどちらか一方です。あいまいな表現をしたのは式の意味さえ分かっていればどちらでも良いためです。上記の式を次のような標準固有値問題に置き換えるという教科書的な説明がよくされています。
$$ A^{\prime} x= \lambda x \\\ A^{\prime} = { ( L^{-1} ) }^{T} A L^{-1}$$
このL行列はB行列をコレスキー分解した時の三角行列で、この \(A^{\prime} \) の対称性を保つための説明は定番となっています。Bの逆行列を掛けて標準固有値問題とすることもできますが、その方法で作成すると \( A^{\prime} \) は一般的に非対称行列になります。非対称になると使えるアルゴリズムが限られてくるのと、メモリ効率が悪くなるためコレスキー分解する方法が良く行われます。もちろん、気にしなければそのまま逆行列を掛けて標準固有値問題にしても答えは同じです。昔はPCのメモリの容量が少なく、そもそも大規模な問題が解けなかったためか、古いソースコードを見ると上記の変換をしてからヤコビ法、ハウスホルダー変換バイセクション法というような実装が多い印象です。
固有値が大きい順とは?
ここで固有値の大きさの順番について考えてみます。基本的な1質点の固有周期の公式を見てみます。$$ T = 2 \pi \sqrt{\frac{M}{K}} $$
この平方根の中の \( \frac{M}{K} \) が固有値です。つまり、この場合は大きい固有値は周期が長くなります。しかし、前述の一般化固有値問題から標準固有値問題に変換する時に質量マトリクスをコレスキー分解、もしくは、逆行列として扱った場合は \( \frac{K}{M} \) として考えたという事になるので、固有値は先ほどの逆数となります。
大小関係も反転するため、剛性マトリクス、質量マトリクスのどちらを分母側で扱うかで標準固有値問題の \( A^{\prime} \) 行列の固有値の大きい方からの順番が入れ替わるわけです。
知りたいのが大きい順なのか、小さい順なのか
前述の通り、建築では固有値が大きい順というよりは固有周期が長い方から順番に欲しくなります。そうなると質量マトリクスをコレスキー分解した場合(パターン1)は標準固有値問題の固有値が小さい順に、剛性マトリクスをコレスキ ー分解した場合 (パターン2) は固有値が大きい順に欲しいというわけです。
インターネットの説明を見ていてもコレスキー分解をするという説明はよく見ますが、 剛性マトリクス なのか質量マトリクスなのかは記載されていない事が多いです。
建築では質量マトリクスを対角行列として扱う事が多いので、コレスキー分解が対角成分の平方根そのままにできるということで質量マトリクスをコレスキー分解するという説明も見ます。
ただ、大規模なモデルのためサブスペース法などを使う時に大きい方が求まるのか、小さい方が求まるのかを意識しないと何次まで求めても、影響の大きいモードが全然出てこないという事態に陥ります。
個人的には、質量マトリクスをコレスキー分解するのは小さいからn個だけを求めるために手順が増えますし、整合質量マトリクス(非対角項にも値がある対称行列)を使っている場合は上記のメリットもなくなるので、剛性マトリクスをコレスキー分解する方が楽に感じています。

閑話
サブスペース法のアルゴリズムが掲載されている本は最近の書籍ではあまり見ないのですが、割と新しい本では同時反復法というアルゴリズムをサブスペース法として載せられている例を見たことがあります。同時反復法は、「べき乗法」という最大固有値に対応する固有ベクトルが1つだけ求まる解法の拡張版です。しかし、厳密にいうと「サブスペース法」と「同時反復法」は区別される風潮が昔はあったみたいです。本質的には考え方は同じと思いますが、 同時反復法は変換した標準固有値問題を解くアルゴリズムであって、サブスペース法は開発者のK・J・Batheが考案した標準固有値問題に変換せずに、一般化固有値問題を解くアルゴリズムを指すようです。 Batheはサブスペース法の開発のために、ヤコビ法を拡張して一般化ヤコビ法というアルゴリズムを開発して、サブスペース法の流れに組み込んだようなので当時の人は流派を明確にしたかったのでしょうか。ソースコード上ではぱっと見でやっていることは違うので区別されること自体は納得できます。1970年頃の話ですがご存じの方がいたらコメントをいただけると幸いです。まとめ
固有値解析のプログラムを自作する場合にはこのような事を意識しないといけません。教科書には載っていないように思えるのでやってみて初めて考えることだと思います。数値解析ライブラリが増えたこの世の中において自作で固有値問題や連立方程式を解くことは稀かもしれませんがこういう経験も意外にソルバ開発の面白さだと思います。Pythonでlinalg.eig関数などを使う場合に引数の質量マトリクス、剛性マトリクスの順番で固有値の並びが変わるところでも確認できますので興味がある方は試してみてください。※ただ、 linalg.eig関数は仕様なのかそもそもの固有値の順番が謎の場合があるようです。
採用情報
構造計画研究所 RESPチームでは、いっしょに働いていただけるエンジニアを募集しています。
構造設計・構造解析だけでなく、プログラミング技術を活かして新しいものを生み出したいと思っている方、ぜひご応募ください。
採用HPはこちら→https://www.kke.co.jp/recruit/