【RESPチーム四方山話】不安定でも解く（3）～一般解と解の存在判定～ |

前回までのあらすじとアジェンダ

前回、連立方程式の解の種類「正則」「不定」「不能」について記述しました。

正則：答えが唯一に求まる（不安定な箇所が一切ない）
不定：答えが複数存在する（不安定な箇所があるけど、外力のかけ方によっては解ける）
不能：どうやっても答えが存在しない（不安定な箇所があり、解くことができない）

その内容を数式にしたらどうなるかを説明します。その後に解が存在する場合にはどのように数式で判定すればよいのかという事について記載していきます

連立方程式の一般解

「正則」「不定」については解が存在します。この解の状態を１つの数式で表すと次の様になります。

$$ \{ x \}_{一般解} = \{ x_0 \}_{特殊解} +\alpha \times \{ x_{n} \}_{余解} $$

「特殊解」は連立方程式を成立させる解で、「余解」は連立方程式の成立には一切影響しない解です。一切影響しない理由としては係数行列を掛けると零ベクトルとなるため、何倍しても零ベクトルとなり解の成立に影響しないという事です。つまり、余解は核（カーネル）に属するベクトルです。例えば、ある不定解が存在したとして、その一般解に剛性マトリクスをかけると次の様になります。

$$
\begin{align}
[K] \{x\}_{一般解} & = [K] \{ x_0 \}_{特殊解} +\alpha \times [K] \{ x_{n} \}_{余解} \\\
& = \{F\} +\alpha \times \{ 0 \} \\\
& = \{F\}
\end{align}
$$

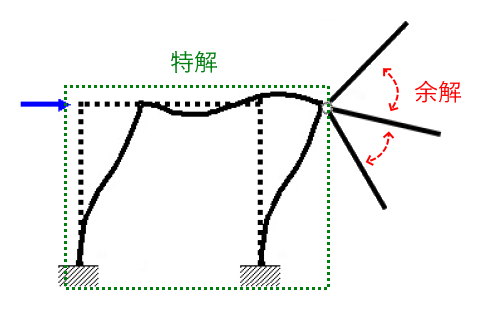
一般解は前回の記事で「不定のイメージ」という見出しに記載した内容を数式で表わしたものです。絵で書くと次のようなイメージです。係数αは余解の分だけ動かしている部分に該当します。

解の存在について

説明がまどろっこしくなってきましたが、連立方程式の「解が存在する」とはこの「一般解が存在する」という事に他なりません。こんどは解が存在しない場合を考えてみます。次のような解析をイメージしてください。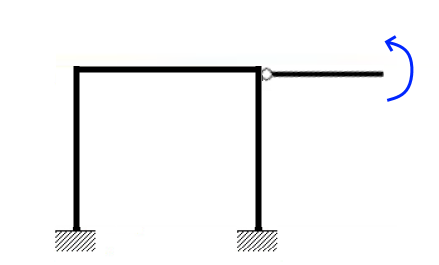

カーネルとなる変位が生じる外力を作用させている状態です。つまり応力が発生しません。このシリーズの一番最初の記事でも記載しましたが、剛性方程式で左辺側の内力が発生しないので、それに対応する外力は再現することができないので、この場合は解が存在しません。
逆に言えば、外力に対応する応力が「漏れがなく」発生する場合はつり合いがちゃんと取れるので、それが解が存在する条件と言えそうです。その外力を分解した時にカーネルに属する変位を含んでいる場合は内力を再現できないので、「不定」となる条件は「解析結果にカーネルを一切含まない」という条件が必要です。
以下で言えば、青実線の通りに外力を掛けた場合、水平の青点線部分に関しては連立方程式でつり合いが取れますが（※座屈は考えません）、赤点線部分についてはカーネルに属する変位を生じるので「不能」となります。

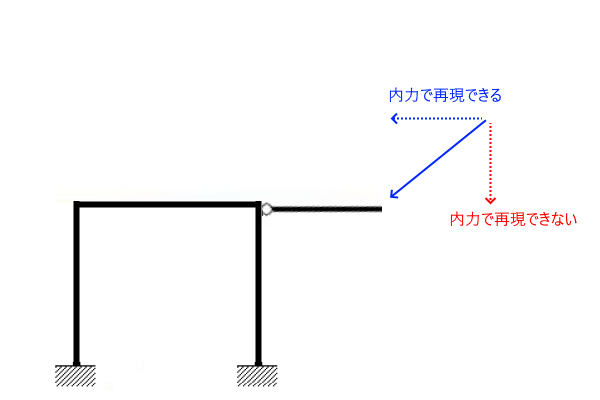
数式による解の存在判定方法

前述の絵で「内力で再現できない」成分が全くない状態であれば一般解が存在するという事になります。ここでようやく「一般化逆行列」の出番です。一般化逆行列の定義は次の通りです。
ある行列$ [A] $に対して次の4つの条件を全て満たす$ [A]^{\dagger} $のことを一般化逆行列と呼びます。

$$
[A] [A]^{\dagger} [A] = [A] \\\
[A]^{\dagger} [A] [A]^{\dagger} = [A]^{\dagger} \\\
([A] [A]^{\dagger})^{T} =[A] [A]^{\dagger} \\\
([A]^{\dagger} [A])^{T} =[A]^{\dagger} [A] $$

細かい話をするとこれは「ムーア・ペンローズの一般化逆行列」と呼びます。この４つの条件を何個満たしているかで名前が変わります。ただ、通常は「ムーア・ペンローズの一般化逆行列」の事を「一般化逆行列」、「疑似逆行列」と呼ぶことが多いようです。そして、この「一般化逆行列」はそもそもAが正則であるなら普通の逆行列となります。※$ A^{\dagger} $を $ A^{-1} $ に置き換えて考えてみれば全て成立することがわかります。
この一連の不安定構造の解析には正方行列として使いますが、一般化逆行列自体は長方行列に対しても存在するのでいろんな分野で利用されています。
求め方は特異値分解をする方法がよく使われます。Python、Juliaなどではpinvという関数が標準で用意されているのでこれを使えば簡単に求めることができます。解の存在条件は剛性マトリクスの一般化逆行列を用いて次の様に表せます。
剛性方程式$ [K] \{X\} = \{F\} $に対して次の条件を満たす場合は一般解が存在します。

$$ [I - KK^{\dagger}] \{F\} = \{ 0 \} $$

この式は外力$F$がカーネルに属する変位を生じないという事を表しています。
そして、この一般解自体は次の様に求められます。

$$ \{X\} = [K]^{\dagger} \{F\} + \alpha \times [I - KK^{\dagger}] $$

この右辺の第1項の$[K]^{\dagger} \{F\}$が以前の記事で「実現象をそのまま解析する」の見出しに記載した解そのものとなります。繰り返しになりますが、$K$が正則であるなら $ K^{\dagger}$ の部分が $K^{-1}$と考えれば第2項はキャンセルアウトするのでいつもの見覚えのあるの連立方程式となります。この辺の数学的な理解は線形代数の細かい話になり、いろんなサイトでも解説があるのでこのブログでは記載を省きます。

閑話

今回、一般化逆行列の記号を右上添字の $ \dagger$ で表しました。本によっては、$+$ で表現されることもあります。自分で記事を書いてみて初めて知ったのですが「短剣符」と呼ぶそうです。この記号は「共役転置」（行列を転置して複素数が共役複素数となる）を表すこともあります。逆に「共役転置」自体は右上添字を $*$ で表すこともあります。
虚数も$i$や$j$で表すことがあるように、分野によって傾向が違うのか、先日とある処理のプログラムを書いていて、深く考えずに「一般化逆行列」を「共役転置」と読み違えて意味が分からなくなってしまいました。
展開の流れをよく読んだら間違いに気づきましたが、紛らわしいので短剣符を見つけた時は注意して式を眺めた方がよさそうです。

まとめと次回予告

今まで感覚的に不安定の議論を進めてきましたが、数式的に判断する方法を紹介しました。プログラムで処理する時は「ムーア・ペンローズの一般化逆行列」を使えば、「正則」であっても「不定」であっても問題を解くことができます。ただし、処理スピードを考えると、汎用化のために全ての解を一般化逆行列を使うのではなく、通常の逆行列が存在するならそちらを使った方が良いと思います。
次回は実際に「ムーア・ペンローズの一般化逆行列」を使って不定な問題を解いてみることにします。

採用情報

構造計画研究所 RESPチームでは、いっしょに働いていただけるエンジニアを募集しています。
構造設計・構造解析だけでなく、プログラミング技術を活かして新しいものを生み出したいと思っている方、ぜひご応募ください。

採用HPはこちら→https://www.kke.co.jp/recruit/