過去のブログにおいて、汎用応答解析プログラムRESP-F3Tとプログラミングを組み合わせたダンパー設計の自己補正の検討を実施した結果を紹介しています。過去記事でも紹介した通り、RESP-F3Tはテキスト形式入力で解析条件、解析モデルを定義する仕様であることから、様々なプログラミング言語などと組み合わせた検討により、任意の様々なパラメトリックスタディが可能です。一方、近年では設計業務においても最適化手法などを用いたパラメトリックスタディが活用されるようになっています。そこで、今回は、過去のブログで扱ったものと同様の超高層建物の振動モデルを対象に、RESP-F3Tに対し、多目的最適化手法を活用したダンパー設計のパラメトリックスタディに関する分析事例を紹介します。
実施概要
設計では、任意の指標を複数考慮しながら設計解を判断することがよくあると思います。そこで、本検討におけるパラメトリックスタディでは、複数の指標を目的関数とした多目的最適化手法の検討を行います。検討の流れは以下の通りとなります。
- ダンパーを付加する前の架構を等価な多質点曲げせん断モデルに置換し、RESP-F3Tのインプットファイル(ftcファイル)を作成
- ダンパー設置対象とする層、層グルーピング(設計変数)の設定
- 各設計変数に対して、パラスタ時に選定対象とするダンパー諸元の選定候補リストの設定
- 設計における分析指標(目的関数)を複数設定し、多目的最適化の汎用フレームワークを適用
- ダンパー設計候補解のRESP-F3Tによる応答解析に基づく各設計解の目的関数の評価
- 多目的最適化に基づくパレート最適解の評価
今回は、過去ブログで作成した制振モデルを対象とします。本ブログにおける多目的最適化計算を前提としたパラメトリックスタディでは膨大な数のモデルの時刻歴応答解析の実施を想定することから、立体解析モデルと比較して、計算コストの小さい多質点曲げせん断モデルを対象とした検討を行います。多目的最適化計算においては、解析入力ファイルにおける制振ダンパーの諸元のみを書き換えた、膨大な応答解析計算による応答評価結果から、任意の設計指標を最小化するダンパー配置を探索します。
実施内容
以下では、上記のフローの実装において考慮したポイントをいくつか示します。なお、本検討においては、プログラミング言語は一般的によく用いられているPythonを用いました。
①多目的最適化について
最適化というと、ある指標を想定したときに、その指標に対して最も性能の良い解を選ぶという印象を持たれるかもしれませんが、任意の目的関数、設計変数を想定した多目的最適化計算を行うことで、複数の指標をともに最小化するような多目的最適解を複数得ることができます。設計では非常に膨大なパラメータを考えながら、各設計指標を平均的によくするような設計解を複数の設計候補解を見比べながら考えたいと思うことがあるかと思います。そうした場合の検討として親和性が高い手法と考えられます。
多目的最適化アルゴリズムとしてはNSGA-Ⅱを想定します。本アルゴリズムは、多点探索の発見的手法(メタヒューリスティクス)の一種である遺伝的アルゴリズム(GA)を、複数の目的関数を有する問題に適用可能に拡張したものです。本検討では、多目的最適化のライブラリとしてオープンソースツールとして公開されているOptuna(https://optuna.readthedocs.io/en/stable/index.html)を用います。発見的手法(メタヒューリスティクス)は、大域的な探索ができる一方、解の収束判定が難しいという特徴があります。したがって、数値的に厳密な最適解を求めることは難しいのですが、ある程度のところで収束しているものとみなして計算実行を止めることで、厳密な最適解でなくとも、ある程度の最適解を得ることができるという点では、設計との親和性が高い手法と考えられます。一方、収束までにどの程度の計算が必要かどうかは、対象とする設計問題の性質により異なるため、対象問題に応じた計算パラメータの個別設定が必要です。
なお、GAによる最適化計算においては、1世代において設定した個体数分の目的関数についての評価計算を行い、次世代に向けて選択、交叉、突然変異の遺伝的操作を各個体に対して適用し、次世代の評価対象個体を生成します。その繰り返し計算を続けて行うことで、解を徐々に最適解に近い解に収束させていく方法になります。したがって、解を収束したものとみなすまでに計算を何世代行うかもユーザー側が定義することになり、解が収束傾向にあることを確認の上計算を止めることになります。この際、「世代間において、最適解の性能評価値の値が変わらない回数が⚪︎世代続いたら計算を終了する」などの考え方で収束判定などを行うこともあります。GAについては、1世代あたりの個体数にも得られる解が依存したり、選択手法や交叉手法についても色々あり奥が深い部分はありますが、その辺りの細かい説明については本ブログでは割愛します。
②応答解析計算の連続実行について
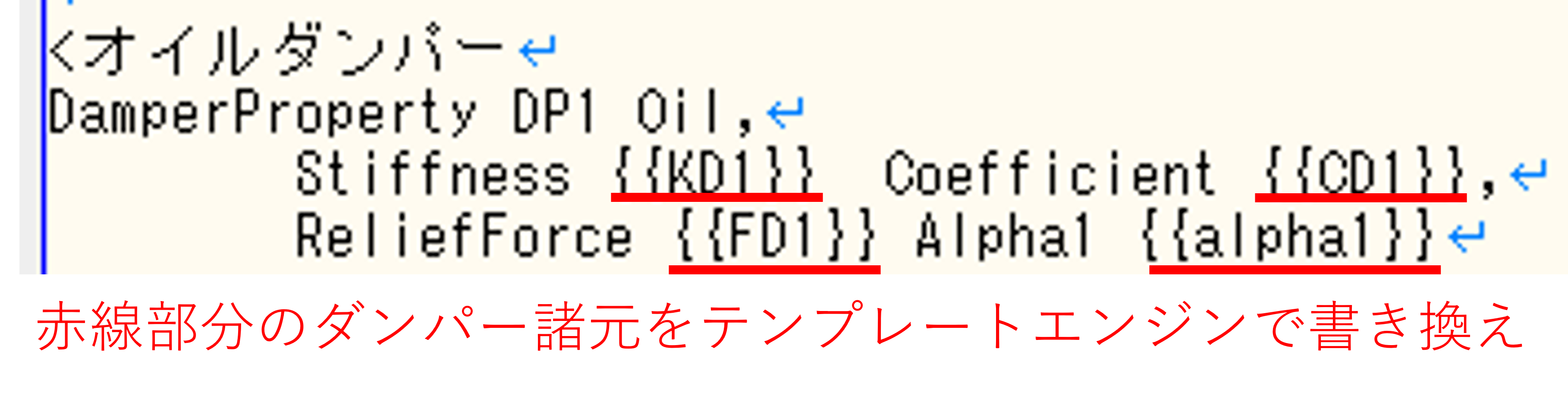
設計解のパラメトリックスタディにおいては、対象とする様々なダンパーの剛性、耐力を想定した場合の地震応答値を評価するため、それらのパラメータを書き換えたRESP-F3Tの入力ファイルを作成・実行する操作をプログラムにより繰り返します。この操作を行う上では、テキストファイルの必要箇所のパラメータのみを書き換えることが可能なテンプレートエンジンを用います。テンプレートエンジンによる応答解析の入力ファイルのテキスト書き換えにおいては、過去ブログでも詳しく紹介されていますのでご覧ください。今回もブログで紹介されていたjinja2というライブラリを使います。
このライブラリを用いると、図のように入力ファイルの変えたい箇所をテンプレートとなるテキストファイル上であらかじめ定義することで、指定した箇所をプログラム側で操作し任意のパラメータで書き換えた入力ファイルを作成することができます。図に示すのは、バイリニア型のオイルダンパーの非線形特性を定義している部分であり、ダンパーの剛性や減衰係数、リリーフ荷重などをテンプレートエンジンで書き換えた上で、入力ファイルの応答解析計算をバッチ処理で実行させ、各設計解の応答値を評価します。
解析結果
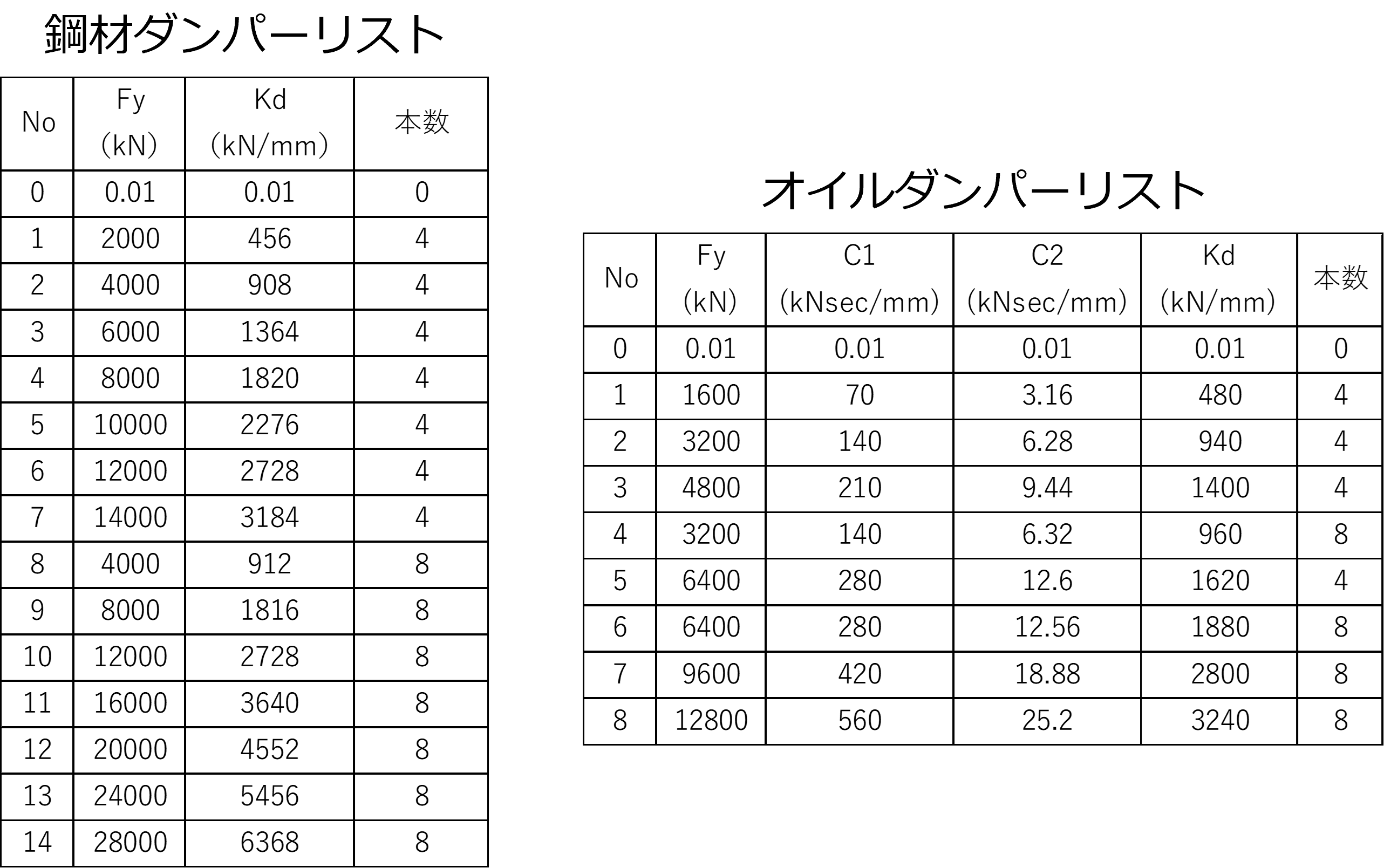
前回ブログで扱った50層の例題モデルを想定した分析結果を示します。応答評価における対象地震波はBCJ-L2を想定します。設計における配置ダンパーとして、オイルダンパーを対象とし、モデル全層を配置対象層とします。ただし、本解析ケースでは設計変数を減らし解の収束を速めるため、ダンパー配置は5層分で1グルーピングを仮定します。その場合、ダンパー設計解としての設計変数は1モデル当たり10個となります。パラスタにおける選定候補とするダンパーリストにおいては、現実的なダンパー諸元と層当たりの配置基数から仮定し、表で示す形で設定します。したがって、本検討におけるパラメトリックスタディの際には、あらかじめ指定した表に示すダンパー選定リストから、各グルーピング位置に対するダンパー諸元を選定する流れとなります。
①パレート最適解について
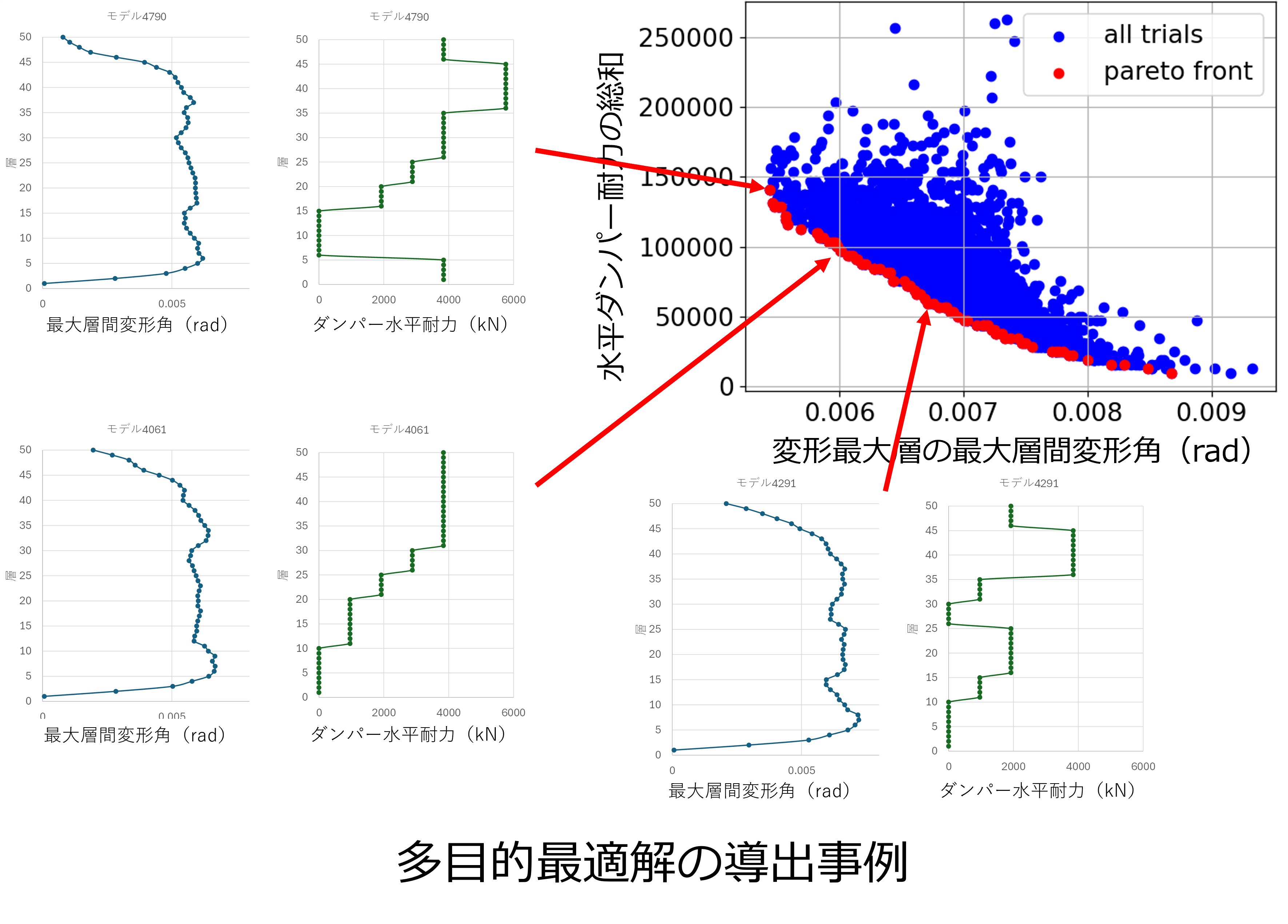
計算により得られた解の見方としては、グラフ中の赤点で表されるパレート最適解に着目します。パレート最適解は、最適化計算の中で得られた設計解の中から、いずれの実行可能解にも優越されない解をピックアップしたものです。グラフの縦軸と横軸はパラメトリックスタディにおいて対象とした目的関数をそれぞれ示しており、グラフ中における一つの点が一つの設計解という見方をします。パレート最適解においては、片方の指標(変形)を下げようとすると、もう片方の指標(ダンパー投入量)が上がるというトレードオフの関係がグラフ的に表現できていることがわかります。グラフの左下にいくほど、2指標を共によくする解であり設計的に妥当な解ということも考えられるかと思います。設計時においては、許容変形の中でコスト最小化を試みることなども考えられ、こうしたグラフを見ながら、妥当な設計解を選んでいくこともできると思います。
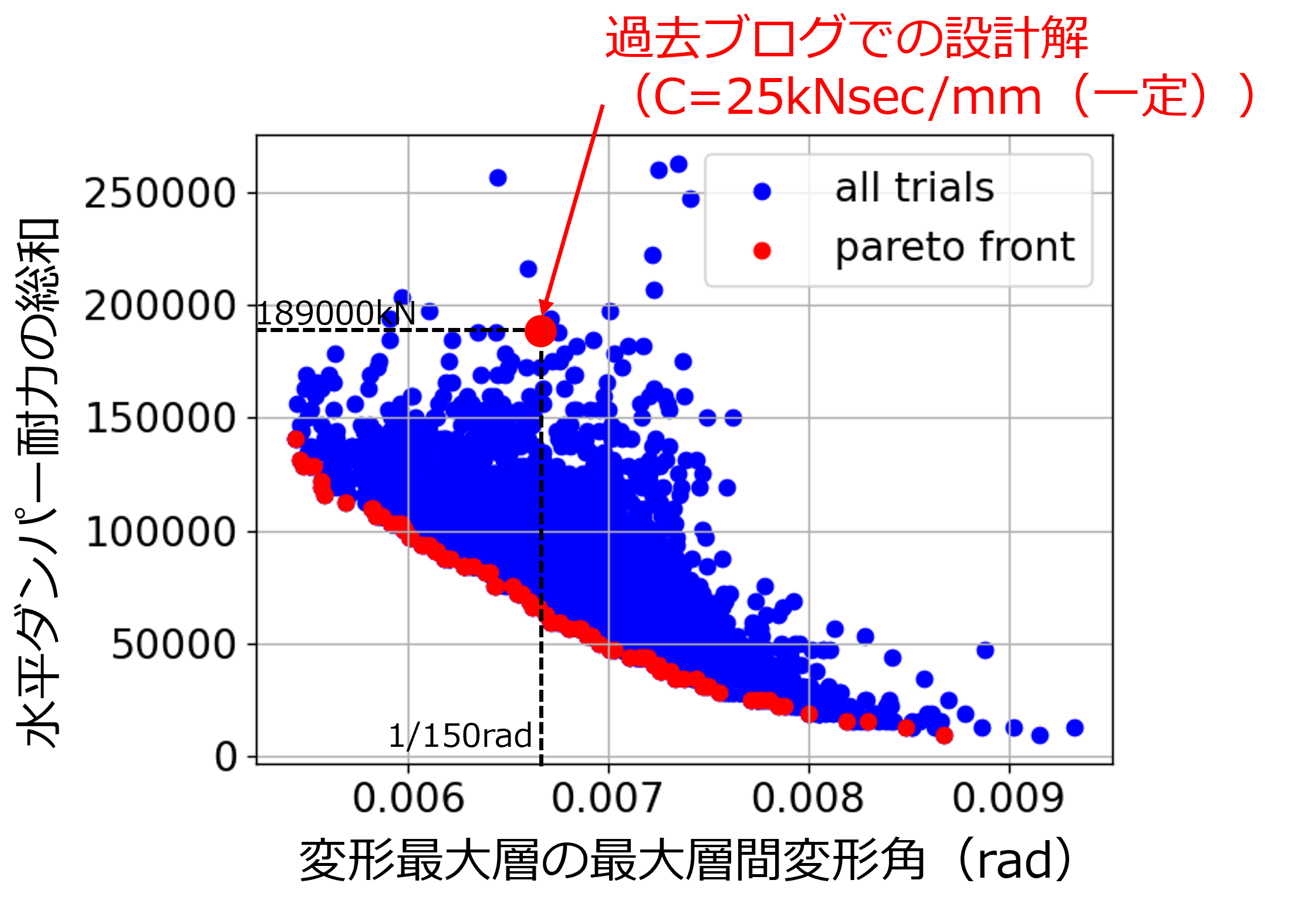
なお、前回のブログで得られた解を本検討で得たパレート解の上にプロットしたものを下図に示します。今回の配置検討対象としたオイルダンパーの減衰係数(17.5kNsec/mm~70kNsec/mm)と前回の検討オイルダンパーの減衰係数(25kNsec/mmで一定)と比較すると、今回の方が選定対象としたオイルダンパーの減衰係数がやや大きくなる場合もあり、その点で平等な比較はできませんが、目標となる層間変形角(1/150rad)を満たす水平ダンパー耐力は、今回検討で得られたパレート解の方が前回ブログの解に比べ、小さい値として得られていることがわかります。
②計算において設定する世代数に関する考察
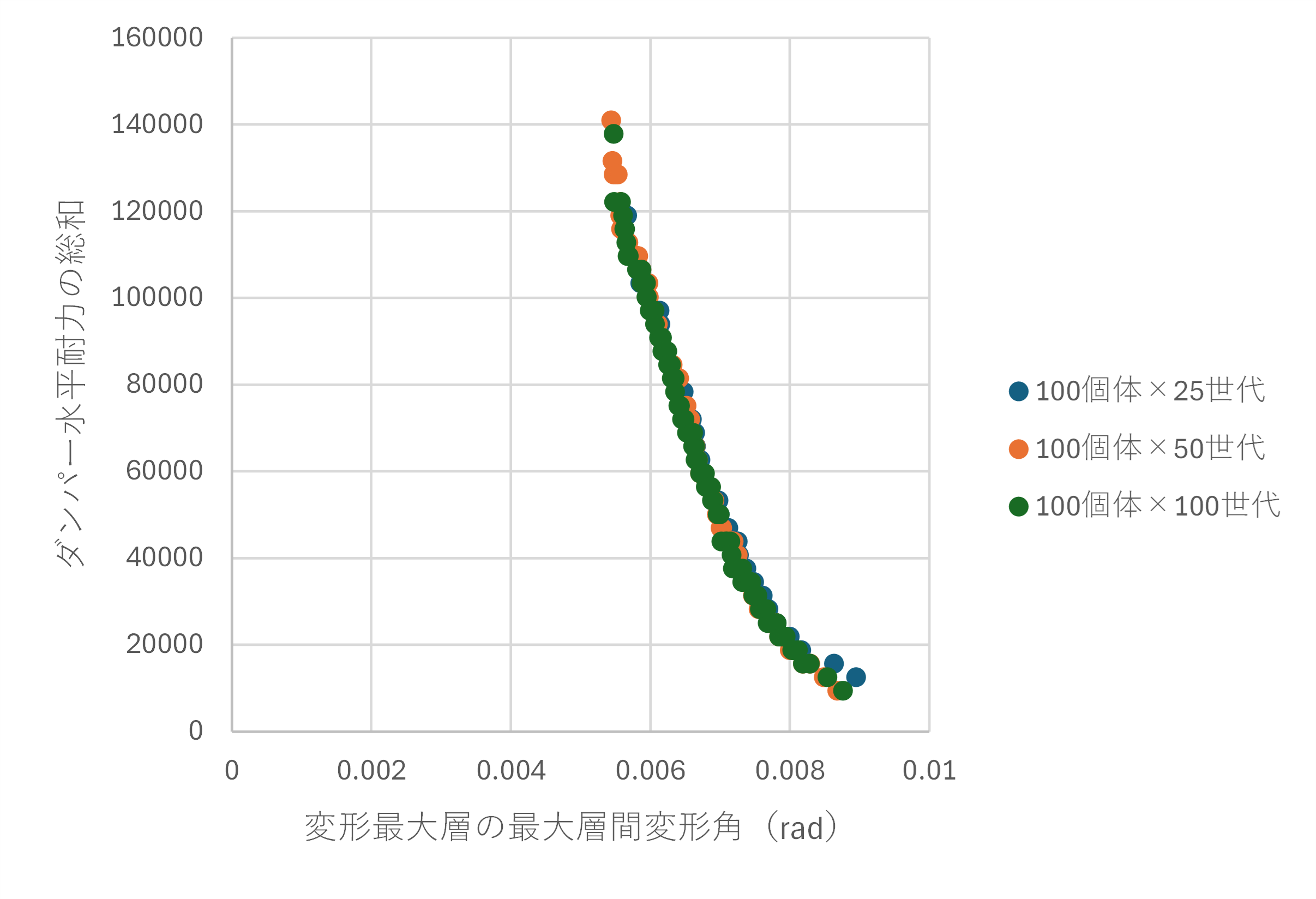
本ケースにおける最適化計算においてどの程度の計算回数が必要かを改めて確認するため、種々の計算回数を想定した解析を行います。発見的手法を用いた最適解を考える場合、対象とする設計解全体の解空間の大きさにおいて、どの程度の量の繰り返し計算が収束解を得るために必要なのかを事前に検討することが必要です。そこで、今回の設計問題において、100個体×25世代、100個体×50世代、100個体×100世代をそれぞれ想定した場合に得られるパレート最適解を下図に比較します。図より、本解析ケースにおいては、いずれも概ね同程度のパレート最適解が得られており、計算回数によらず収束値に近い値に至っていることが考えられます。
なお、本ケースにおいては50質点の曲げせん断モデルを対象に、BCJ-L2(120s)の地震波を想定した時刻歴応答解析を行いましたが、その場合、単位応答解析の計算時間は2.5s程度でした。したがって、上記の事前解析において、最大計算回数(100個体×100世代=10000回)を想定した際には、最大で7時間程度の計算時間を要しました。設計においてはこの辺りも計算コストと得られる解精度との兼ね合いで適宜パラスタを行う必要があり、得られる最適解に大きな差がないのであれば、25世代(計算回数2500回)で計算を打ち切るなどの判断をすることも考えられます。
③パレート最適解を得るための目的関数の設定
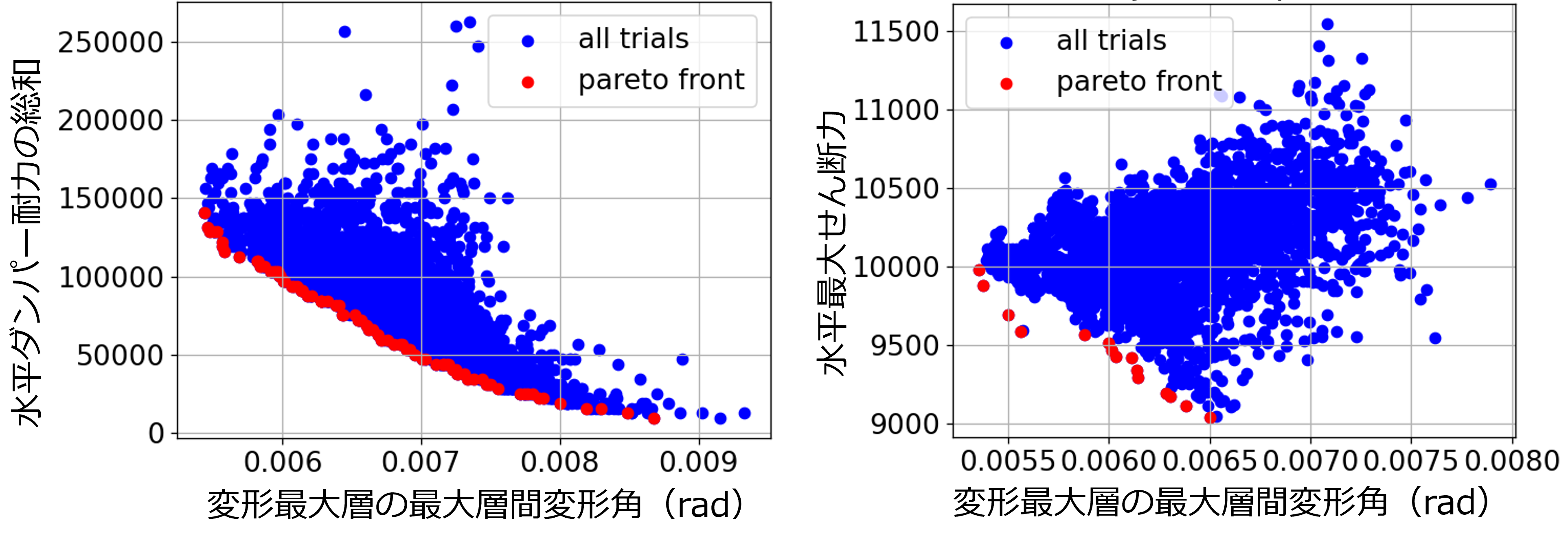
目的関数として、トレードオフの関係になると考えられる最大層の層間変形角と導入したダンパー耐力の総和を設定した結果を示します。また、比較のため、トレードオフの関係になりにくそうな最大層の最大水平せん断力と最大層間変形角を目的関数として設定した解析結果も併せて示します。図より、前者の場合パレート最適解をあらわす曲面がはっきり得られていることがわかります。一方、後者の場合、最終的に得られるパレート最適解の数がやや少なくなっており、幅広く明瞭なパレート最適解を得るためには、適切な目的関数の設定が重要であることがわかります。
④配置対象とするダンパーの種類を変えた場合
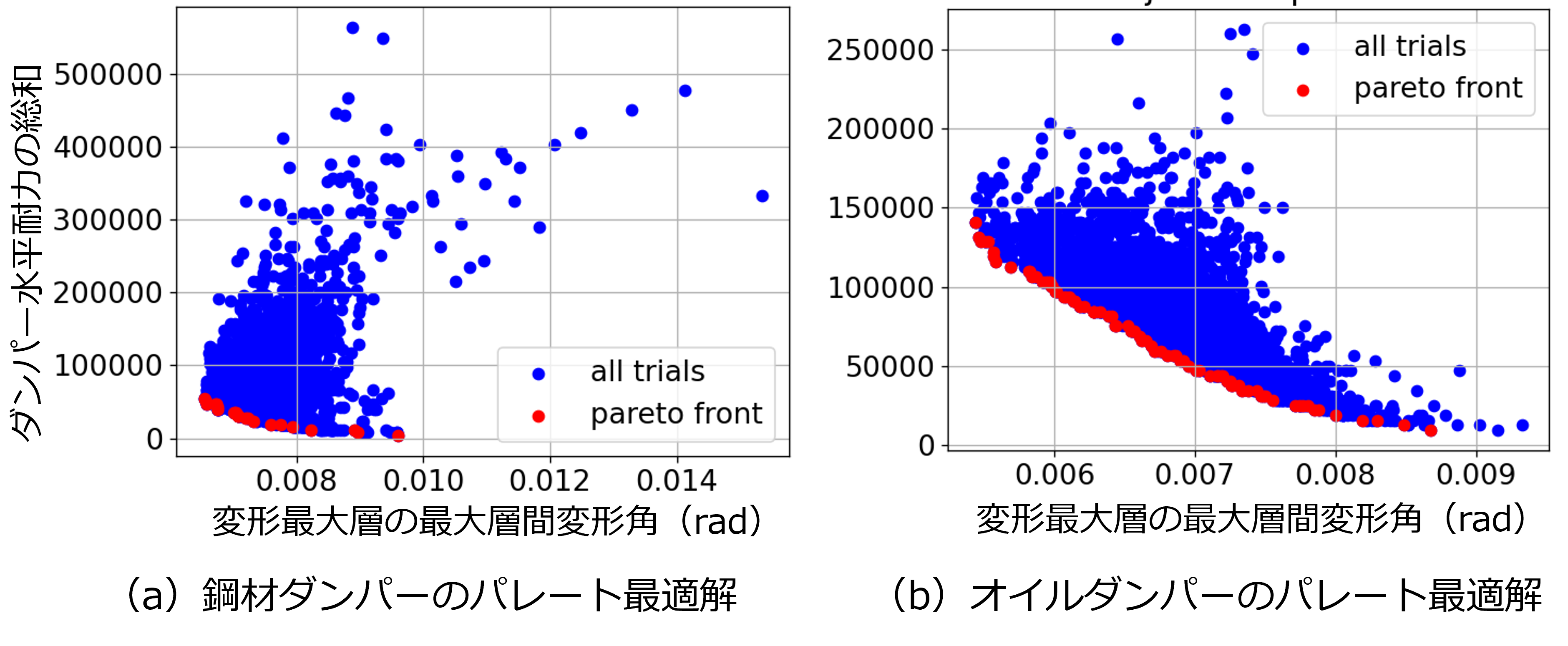
最後にパラメトリックスタディにおいて配置対象とするダンパーとして、鋼材ダンパーを想定した場合の結果をそれぞれ比較します。計算条件はオイルダンパーの検討と同様とします。図より、鋼材ダンパーを配置対象として想定した方が、オイルダンパーを配置対象とした場合に比べ得られる設計解がやや広範囲にばらつき、パレート最適解の総数も少ない傾向がみられることがわかります。
これは、パラメトリックスタディの過程で鋼材ダンパーの水平耐力を増していった場合、ダンパーが降伏しないあるいはダンパーの最大塑性率が比較的小さい領域となるため、常に一定の付加減衰が付与されるオイルダンパーを配置対象とした場合に比べて、ダンパー数増加により得られる付加減衰が小さくなってしまうためと考えられます。したがって、このような剛性・耐力に必ずしも比例しない付加減衰となる変位依存型ダンパーを設計対象とする場合、幅広い範囲のパレート最適解を得るためには、ダンパー選定候補リストの範囲をさらに調節したり、より多くの計算回数を実施することが必要な可能性も示唆される結果となっています。
まとめ
今回は例題モデルを対象に、多目的最適化手法を用いたダンパー設計解の分析を実施した事例を紹介しました。一方で今回分析した形以外にも、対象とする設計問題に応じて様々な目的関数や設計変数の選び方が考えられます。したがって、設計条件に応じた適切な目的関数や設計変数、解析パラメータを設定したパラメトリックスタディを行うことで、様々な設計業務において、設計について幅を持って検討を進めたり、マクロ的な観点での有用な工学的知見が得られる可能性があると考えられます。