今回はその理解のために連立方程式の解の種類について解説します。
連立方程式の解の種類
連立方程式の解は次の3種類あります。- 正則:答えが唯一に求まる
- 不定:答えが複数存在する
- 不能:どうやっても答えが存在しない
正則の場合
正則の場合の連立方程式は次のような場合になります。$$
\left(\begin{array}{cc} {1} & {3} \\\ {2} & {4} \end{array}\right)
\left(\begin{array}{c} {X}_{1} \\\ {X}_{2} \end{array}\right)
=
\left(\begin{array}{c} {3} \\\ {6} \end{array}\right)
$$
$$
{ \left(\begin{array}{cc} {1} & {3} \\\ {2} & {4} \end{array}\right) }^{-1}
=
- \frac{1}{2}
\left(\begin{array}{cc} {4} & {-3} \\\ {-2} & {1} \end{array}\right)
$$
$$
\left(\begin{array}{c} {X}_{1} \\\ {X}_{2} \end{array}\right)
=
- \frac{1}{2}
\left(\begin{array}{cc} {4} & {-3} \\\ {-2} & {1} \end{array}\right)
\left(\begin{array}{c} {3} \\\ {6} \end{array}\right)
=
\left(\begin{array}{c} {3} \\\ {0} \end{array}\right)
$$
このような問題は構造解析で言うところの、不安定な要因が一つもなくプログラムを使っても何の問題もなく解くことができるような状態です。
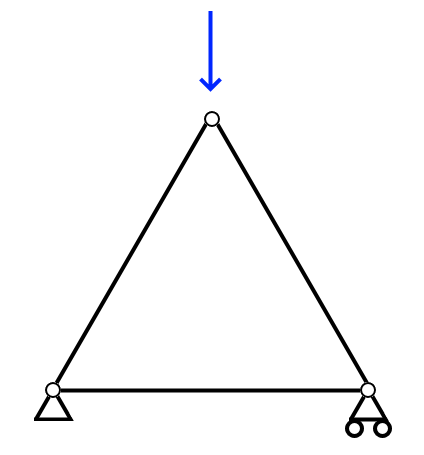
不定の場合
次に不定の場合を示します。$$
\left(\begin{array}{cc} {1} & {2} \\\ {2} & {4} \end{array}\right)
\left(\begin{array}{c} {X}_{1} \\\ {X}_{2} \end{array}\right)
=
\left(\begin{array}{c} {3} \\\ {6} \end{array}\right)
$$
$$
\left(\begin{array}{cc} {1} & {2} \\\ {2} & {4} \end{array}\right)
\left(\begin{array}{c} {3} \\\ {0} \end{array}\right)
=
\left(\begin{array}{c} {3} \\\ {6} \end{array}\right)
$$
$$
\left(\begin{array}{cc} {1} & {2} \\\ {2} & {4} \end{array}\right)
\left(\begin{array}{c} {1} \\\ {1} \end{array}\right)
=
\left(\begin{array}{c} {3} \\\ {6} \end{array}\right)
$$
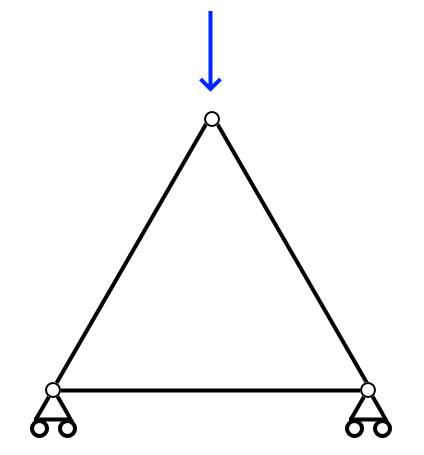
不能の場合
最後に不能の場合を説明します。$$
\left(\begin{array}{cc} {1} & {2} \\\ {2} & {4} \end{array}\right)
\left(\begin{array}{c} {X}_{1} \\\ {X}_{2} \end{array}\right)
=
\left(\begin{array}{c} {5} \\\ {6} \end{array}\right)
$$
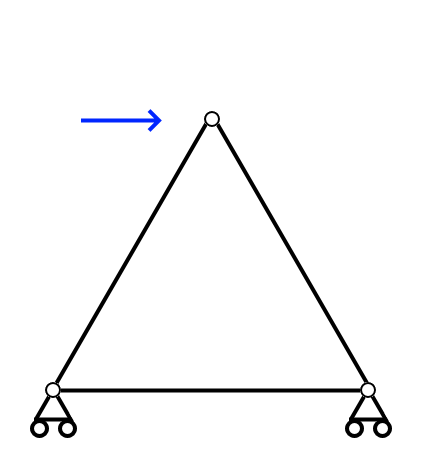
不定のイメージ
不定で解が一つに定まらない事のイメージを説明します。例えば、門型ラーメンに水平力を加えた次のような解析結果をイメージしてください。
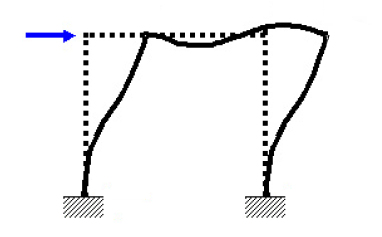
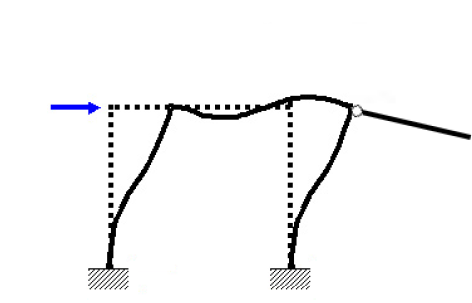
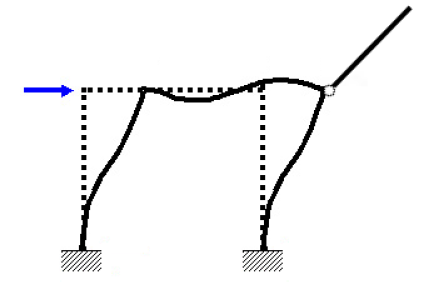
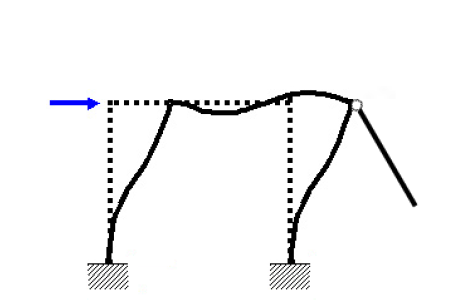
$$
K X = F
$$
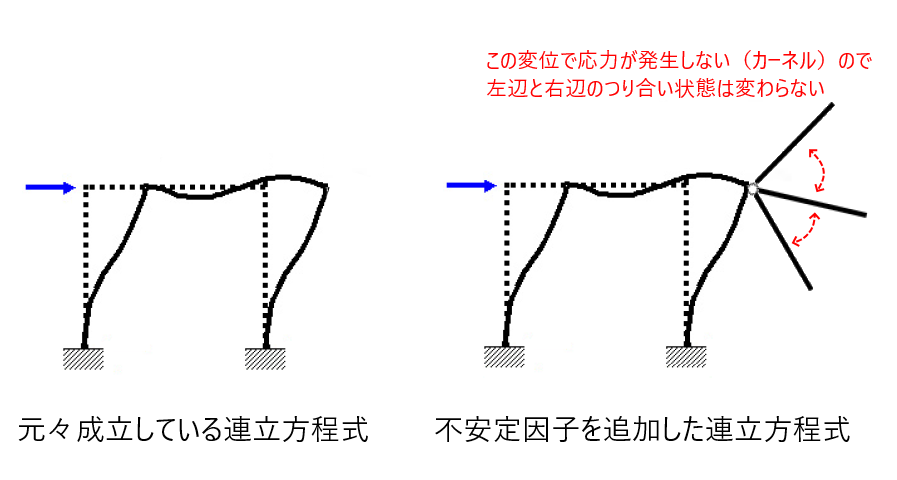
まとめと次回予告
今回は連立方程式の解の種類とそれに対応する構造力学の問題を記載しました。教科書通りに作成したプログラムは通常「正則」の状態しか解けません。市販のプログラムはもっと進んでいて、「不定」な場合は境界条件を変更して「正則」な問題に置き換えるという作業をしています。※この記事も参考にしてください。今回のシリーズはこの「不定」な場合にどうやって判定するか、そして答えをどうやって求めるかという事が肝になります。次回は、連立方程式の一般解と解の存在判定について記載します。