不安定のままでも解ける?
以前、このシリーズの記事で「不安定」とは連立方程式が解けない場合であり、その時の剛性マトリクスには核(カーネル)が存在しているという記事を書きました。しかし、核が存在していても連立方程式は解くことができる場合があります。
何回かにわたって記事にしますが、
今回はイメージをしやすくするためにこれからどんな話をするか説明します。
不安定モデル1
以前のブログでも、外力が作用していなければ、応力状態に影響しないように境界条件を変更して解く事があると記載しました。 弊社製品のRESP-F3Tではそのような機能が付いています。例えば、次のような明らかに不安定なモデルを作成してRESP-F3Tを使って解いてみます。※重力は発生しないとします。
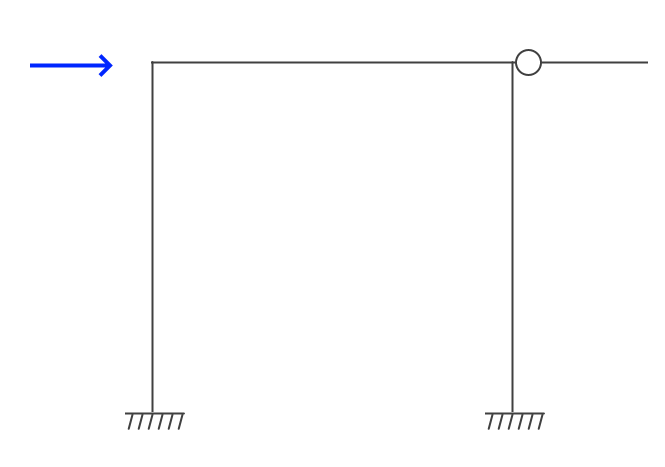
モデル化して解析を流すと、自動で先端部分の回転を拘束して解析を進めてくれます。門型ラーメンのみのモデルの変位に片持ち梁が変位しないような結果なのでイメージ通りです。
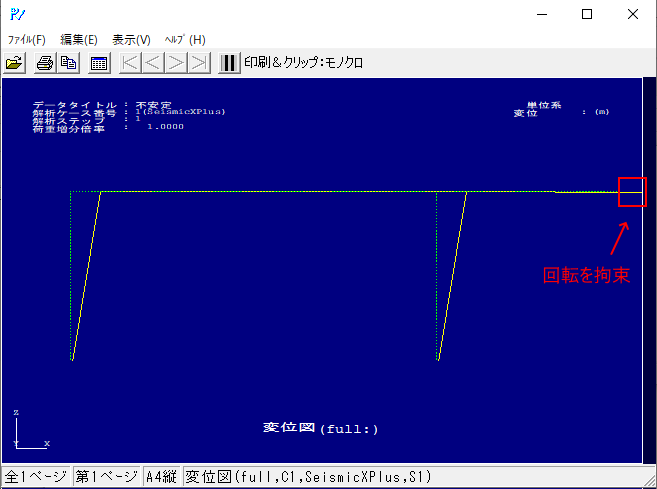
不安定モデル2
では、次に以下のようなモデルを考えてみます。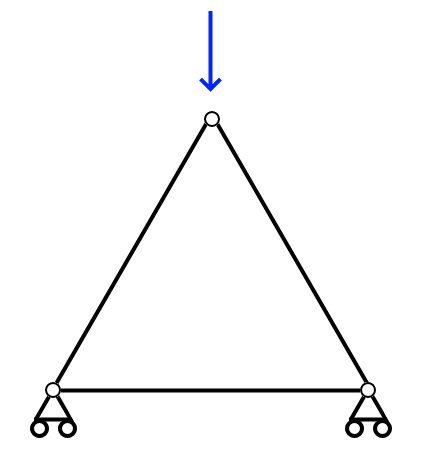
この問題をRESP-F3Tで解くと自動でローラーの片方を水平方向に固定することで解くことができました。
対称なトラスなので頂部の水平移動に対して、ローラーの水平移動が2倍の値となっているので、イメージ通り解けています。
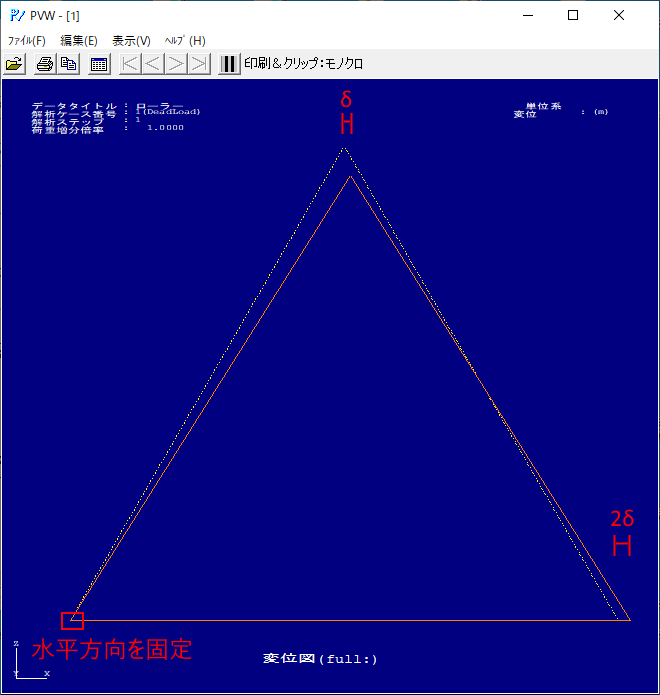
実現象として考えると
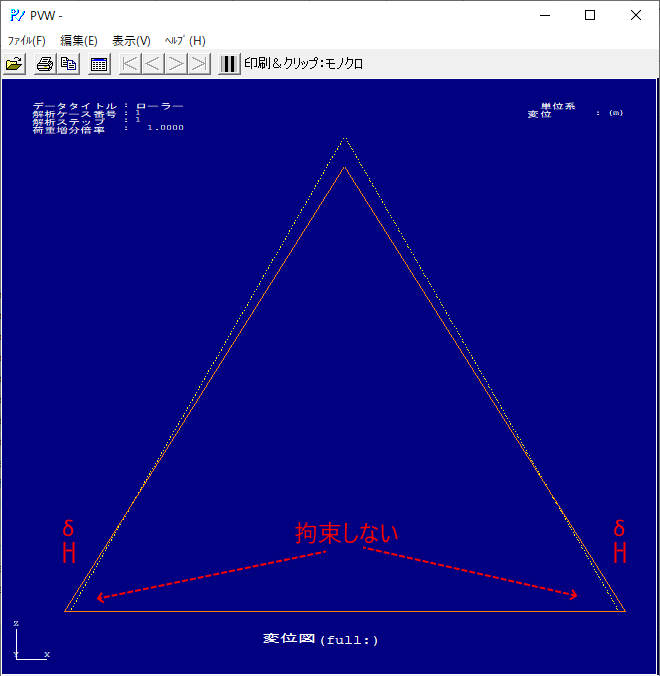
「不安定モデル1」は不安定になる自由度は加えている外力でそもそも変位しないような自由度でした。一方で、 「不安定モデル2」 は拘束したローラーが二つのピン支点のうち他方であれば、示した結果を左右反転した結果になるはずです。つまり、本来変位が生じる自由度を固定していることになります。よって、本当に起きる現象としては解析結果そのままではなく少し調整を加えた次のようなものとなります。
実際にこの問題を模擬するために割りばしで同様のトラスを作って問題を再現してみると次のようになります。
底辺の部材が伸びないと変位しているかがわからないので、厳密にいうと上記解析モデルの様に全て同じトラス要素ではありませんが、イメージの補助になれば幸いです。
建築学科を出ていながらきれいな工作物でなく申し訳ありません。


実現象をそのまま解析する
このように問題を分析して、境界条件を与えて解析を実行して、その結果を適切に調整することで不安定なモデルでも実現象を再現することができます。しかし、この実現象の解を最初から導く方法もあります。つまり、上記のように境界条件を与えずに連立方程式を解くという事です。これを実現するためには一般化逆行列というものを使います。※「擬似逆行列」などの呼び方もあります。