私は昨年の10月にRESPチームに加わりました。前職でも構造計算ソフトの開発をしていたのですが、3年ほど前からRESPブログをよく読んでおりました。新人手記や構造解析Tipsなどを見ていて書いてる人から楽しさが伝わってくるようなコンテンツだなと思っていました。いつか書ける側に回ってみたらこんなこと書いてみたいななどと考えていたら、まさか本当に記事を投稿できる側になって驚いています。
基本的には普段業務をしていて、ある物事をこのように考えたら面白かったとかなどを記述していく感じです。ですので、文体もこのように緩い感じとなっています。厳密さに欠けることもあると思いますが、そんな時はご指摘いただけると幸いです。
テーマは「不安定」
タイトルの通り、今回は私が好きな「不安定」を取り上げてみたいと思います。 ソフトを使って建物をモデル化して、いざ解析を実行したときに不安定となった経験は誰でもあると思います。私は普段解析をしていたり、RESPサポートで不安定に関する内容が来るとうれしくなるのですが、そんな不安定について別の見方をしてみたら面白いのではないでしょうかという提案です。連立方程式が解けない？
そもそも、解析ソフトを使っていて不安定であるとエラーが出るときはどのようなときかをご存じでしょうか。解析実行したときのプログラムの動きをざっくり記載すると次のようになっています。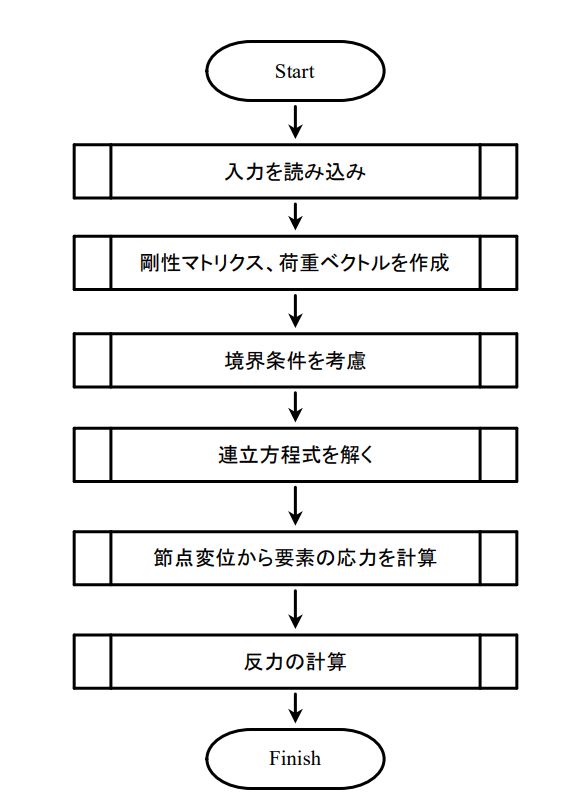
$$ KX=F $$
ここで (K) は全体剛性マトリクス、 ( X) は変位ベクトル、 ( F) は荷重ベクトルです。 不安定とはこの連立方程式を解くことができない時に表示するエラーです。連立方程式が解けないのは係数行列の逆行列が存在しない場合と習うことが多いと思います。※後述の通り、厳密にいうともっと広い範囲で考えることができますが、今回はこれでよいということにします。$$ \mathrm{ det }K \neq 0 $$
逆行列が存在するということを「行列が正則である」といいますが、ここでいうような不安定とは剛性マトリクスが正則ではない状態を指します。 ただし、実際のプログラムでは剛性マトリクスが正則であるかをチェックすることはあまりなく、連立方程式を解きやすい形に剛性マトリクスを分解する時にうまくいかない場合に不安定と判断することが多いです。また、その分解がうまくいかない時でも、その不安定となる自由度に荷重がかからない場合は自由度を拘束して解析を進めることもあります。逆行列を持たない行列の特徴
正則でないN次正方行列の特徴の一つとして核(カーネル)の存在があげられます。核は以下のようにあらわされるような空間です。$$ \mathrm{ ker }K = \lbrace x∈V∣K(x)=0 \rbrace$$
これは「ある行列を適当なベクトルに掛けたら0ベクトルになるような場合が存在した」といった理解で十分です。正則な行列であれば核は0ベクトルのみになります。※行列に0ベクトルを乗じた場合は必ず0ベクトルにります。
正則ではない行列の特徴はいくつかあるのですが、後の説明の意味で一番わかりやすい特徴を選択しました。
構造解析で表現する
ここで、話を構造解析に戻してみます。 応力解析は前述のフックの法則の連立方程式を解いていると書きました。不安定なときは剛性マトリクスの逆行列が存在しない時と書きましたが、その場合は剛性マトリクスに「0ベクトル以外の核」が存在しているということになります。 この時の「0ベクトル以外の核」について考えます。 式で書いてみると次のようになります。$$ KX= 0 ( X \neq 0 ) $$
これは2つの捉え方があると思っていて、一つは何も外力を与えていないのに変位が生じる状態という見方です。これは不安定というイメージと直感的に一致します。 もう一つは、変位を発生させたけど、内力が発生しないという捉え方です。私はこの考え方が好きで、行列の核という観点ではこっちのほうがしっくりきます。構造物は外力を加えない限り状態が変わらないはずです。内力が発生しないような変位がある時は状態が変わっているけど、その時発生している外力が存在しないという見方ができると思います。 つまり、変位させてどの要素にも応力が発生しないような形状が存在する場合、不安定と考えることができます。話をまとめると
今回は記事は建物モデルが不安定となりその原因を考える時に次のように考えると面白いのではないかという提案です。- 構造モデルを観察して、いろいろな形に変位を考える。※この時外力はあまり考えなくてもよいです。
- ある変形のさせ方をすると、建物のどこにも応力が発生しない変位（0ベクトル以外の核）があった。
- 「0ベクトル以外の核」が存在する場合は、逆行列が存在しない。
- よって不安定な構造モデルである。