問題:ある建物で45°加力、135°加力それぞれの層復元力特性を元に作成した質点系モデルで固有周期に差がでました。何故でしょうか?
「45°、135°加力による質点系モデルで固有値に差が生じてしまったが、理由がわからない」。
こういった質問がユーザーサポートに送られてきました。
質点系モデルを作る際には、外力を作用させた結果の層間変位からばねを求めます。通常、弾性範囲では0°方向加力と180°方向加力、90°方向と270°方向加力は変形の符号が反転するだけで変形の大きさは同じになります。45°加力、135°加力は、0°加力と90°加力の重ね合わせとなりますので、この場合も同じばね値になり、固有周期はいっしょになるはずではないか?というのが疑問の発端です。
実際の誤差は、固有周期で1%程度でした。
今回の解答以外にも理由は考えられると思いますが、個人的に発見だったので記事にしました。
ちなみに先に言っておくと答えは、以下ではありません。
- 外力が異なる(応力計算用節点荷重なども含めて)
→今回のケースでは、45°方向加力と135°方向加力で外力のX方向成分、Y方向成分の大きさは同じでした。 - 荷重増分解析の増分刻みが粗く、初期剛性計算時に剛性低下の影響が含まれている
→今回のケースではかなり増分刻みを細かくしても差が小さくなることはありませんでした。 - そもそも建物が傾斜している
→今回のケースでは、基本はX方向、Y方向にラーメン架構を持つ建物でした。
間延びさせてもしょうがないので、先に回答を書きます。
考えている間にネタバレしないように、少し間隔をあけておきます。
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
答え:偏心した建物の場合、加力方向の直交方向の変形が発生し、正負で変形が異なるため
今回の原因はねじれによるものでした。
そもそも、「45°方向加力と135°加力で固有値が同じになるはず」という考えは以下の前提によって成り立っています。
- 45°方向加力、135°方向加力は、それぞれ0°加力と90°加力、180°加力と90°加力の重ね合わせとなる。
- 0°加力と180°加力の解析結果は、符号が反転するだけで結果の数値は変わらない。
- 0°加力と90°加力は、それぞれ0°方向、90°方向にしか変形・応力が生じず、独立している。
この3つめの前提条件が、ねじれが大きい場合には真ではない、ということが今回の原因でした。
ねじれが生じると、加力直交方向に対しても変形・応力が生じます。たとえばY方向加力時にX方向に+の変位が生じたとすると、さらにX方向加力時の変位を加算した値が斜め加力時の変位になりますので、X方向正加力による変位に対しては加算方向となり、X方向負加力による変位に対しては減算方向となります。これにより、同じ大きさの力を加えても、変形に差が生じることになります。
シンプルなモデルで検証
実際にシンプルなモデルで試してみました。
重量をあえて大きく偏心させたモデルを作って45°、135°に加力してみます。
モデルはY方向加力時にねじれが生じるように偏心させてみました。
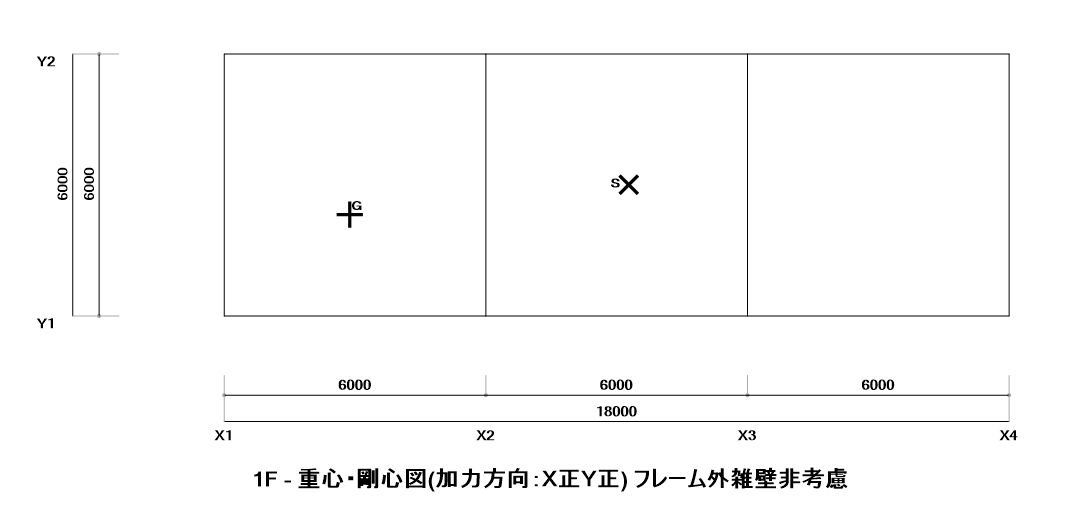
重心(G)、剛心(S)は最下階で以下のような位置関係です。
今回はX,Y方向に偏心を生じさせています。
まずは0°、90°方向に加力
まずは偏心によってどれくらい直交方向変形が生じるか、0°、90°加力を試してみました。
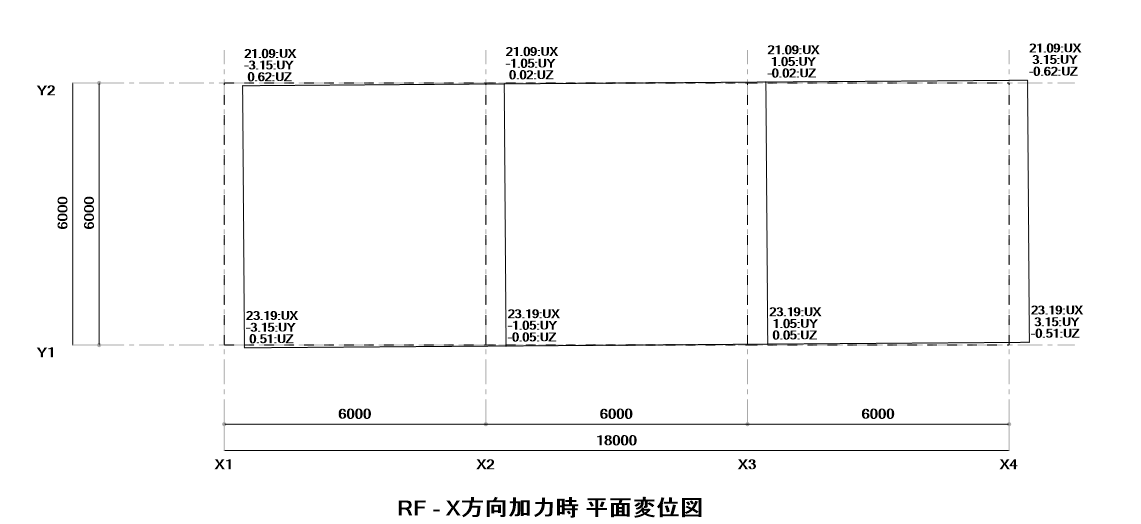
0°加力
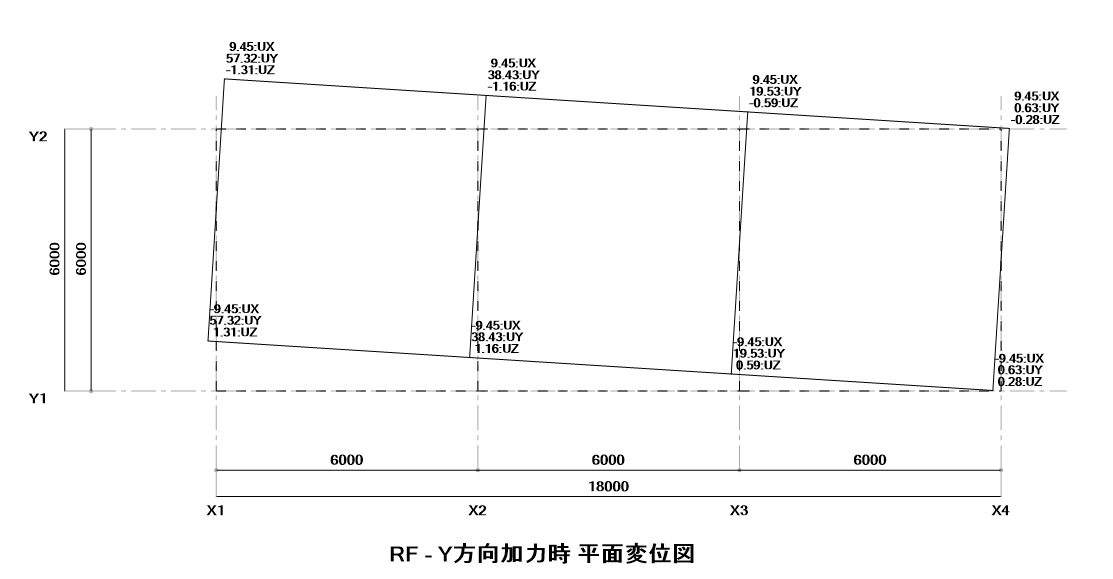
90°加力
着目すべき結果は、重心のY座標はY1通り側によっているので、90°方向加力時に重心位置X方向変位は負側に発生するという点です。
45°、135°加力に加力
斜め方向加力をしてみました。
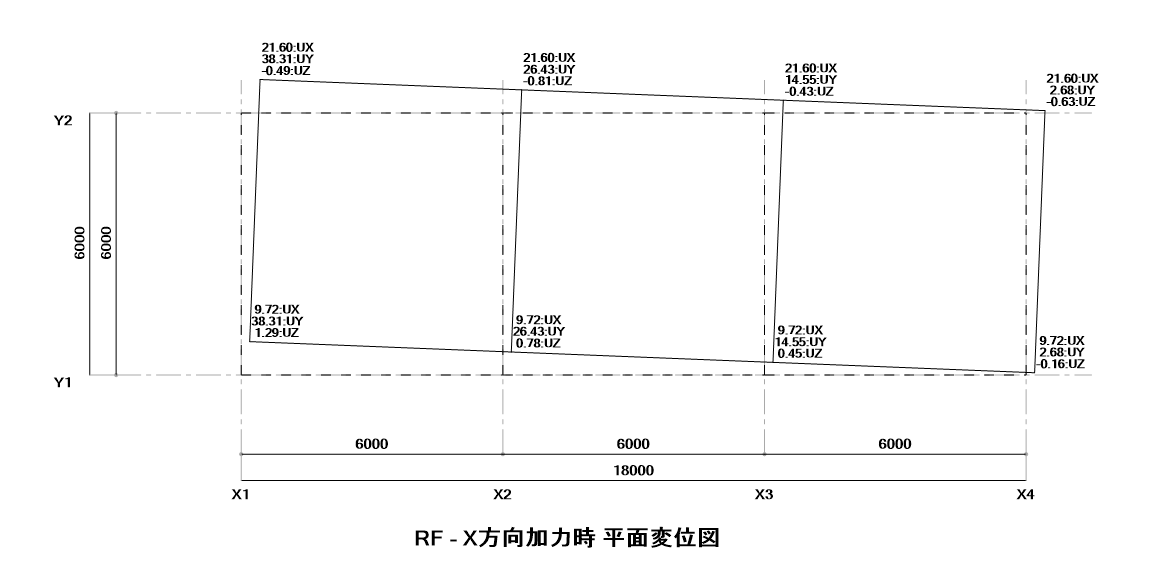
45°方向加力
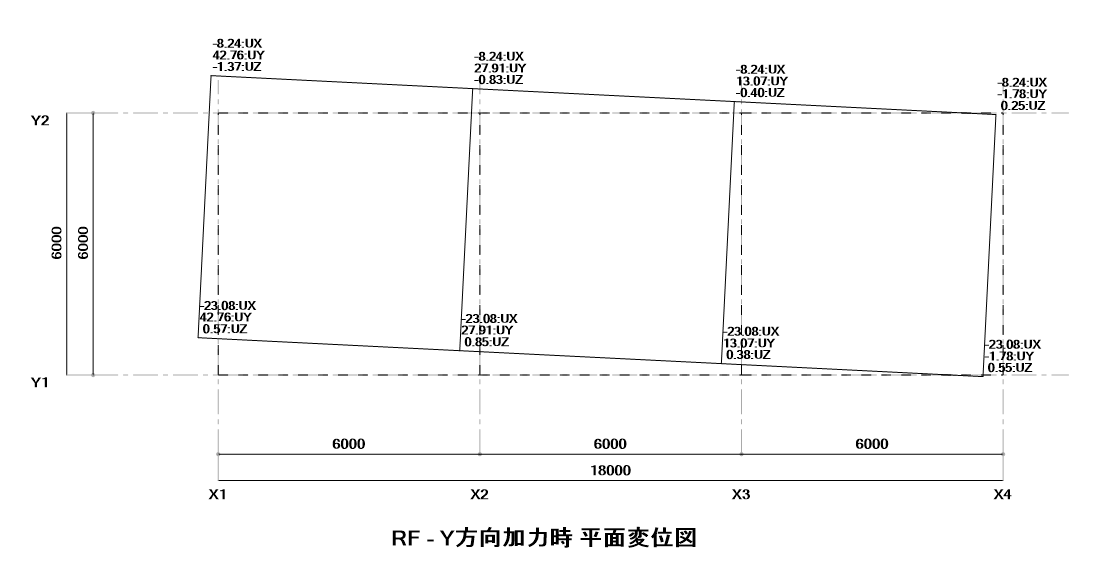
135°方向加力
通常、ねじれがなければ正加力、負加力によって変位の大きさは変わらず、符号が変わってくることになりますが、今回の結果では加力ケースごとに明らかに変位差が生じています。
固有周期は以下のようになりました。
45°加力: 0.6699 s
135°加力:0.7250 s
90°加力により重心位置X方向変位は負側に移動することがわかっているので、X方向負加力のほうが結果的に重心位置変形が大きくなり、固有周期が長くなる、という結果と整合します。
わかってみれば納得ですが、勉強になりました。