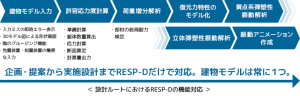
P-Δ効果とは
P-Δ効果とは軸力を受ける鉛直部材が大きな水平変形を受けた場合に、付加応力が発生する現象です。建築構造においては微小変形理論として現象を考えることが多く、かつ線材をメインとして扱っています。そのため軸力がモーメント・せん断力に連成することはあまり考えません。しかしながら、大きな変形の領域になると初期座標≒変形後座標という仮定に誤差が生じ始め、P-Δ効果の影響が無視できなくなります。
地震時に非常に大きな変形が想定される免震部材では、従来からこの影響について考えられてきました。具体的には、P-Δ効果によって生じる付加モーメントを外力として加算し、設計用の付加応力を求めるという方法がよく行われています。
一方、部材に幾何剛性を考慮することで時々刻々P-Δ効果を評価するという方法もあります。
本記事では、外力により付加モーメントを加算する方法と、幾何剛性によって考慮する方法でどのような違いが出るか確認してみました。
なお、以下の記事でもP-Δ効果について検討を行っています。よろしければご参照ください。
2018年度建築学会大会(東北)感想 : 「超高層鋼構造建物のねじれ倒壊メカニズム」についてRESPで検証してみた
解析
解析モデル
解析モデルは1層分の柱と周辺の大梁を反曲点位置まで取り出したような魚骨モデルとしました。
外力は水平力、鉛直力を考慮し、鉛直力は、最大変形時に水平力/軸力=0.2程度となるような値として設定しました。
また、結果をシンプルにするため材料特性は弾性としています。
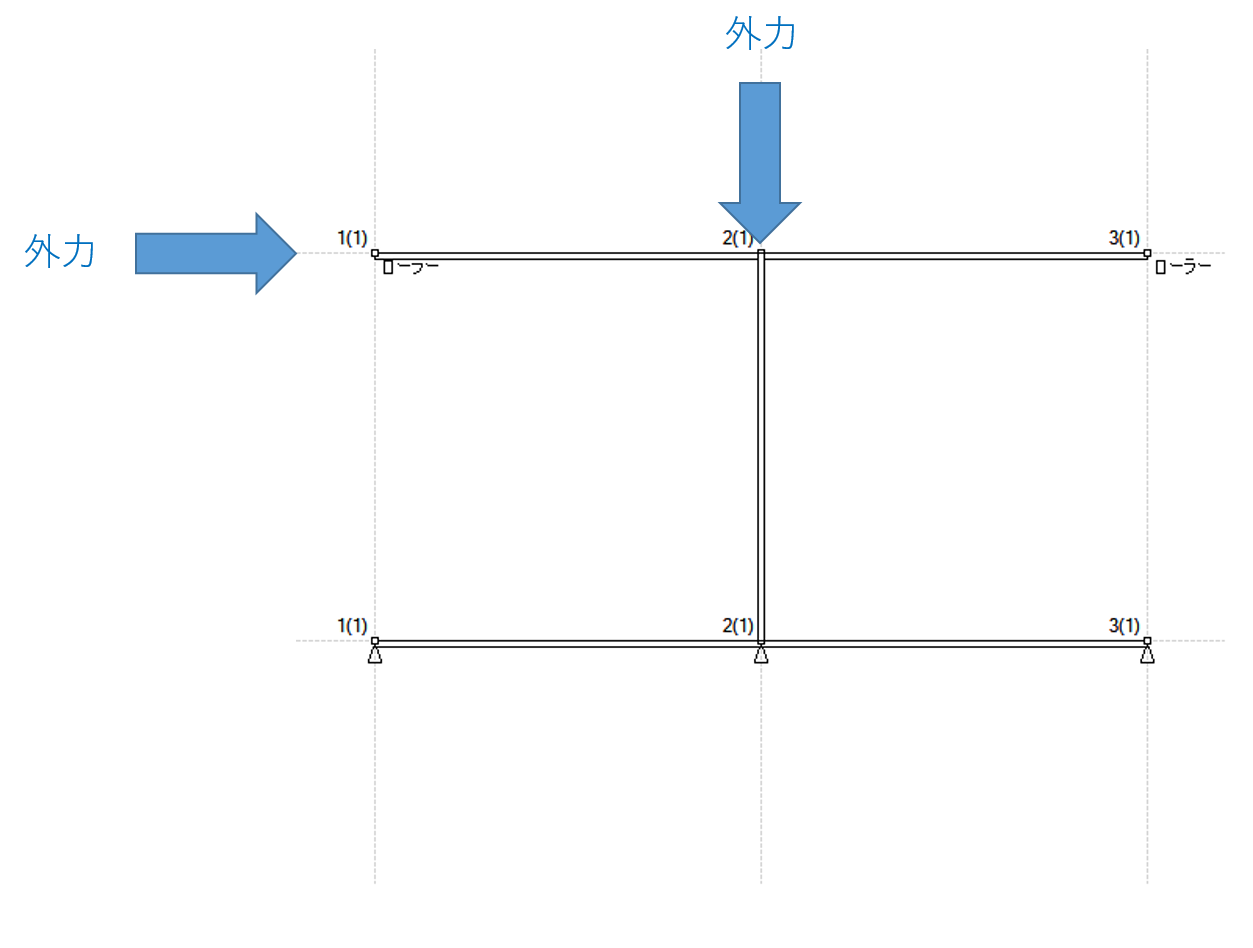
モデル図
P-Δ効果の考慮方法として以下のように付加モーメント考慮と幾何剛性考慮のケースを解析します。
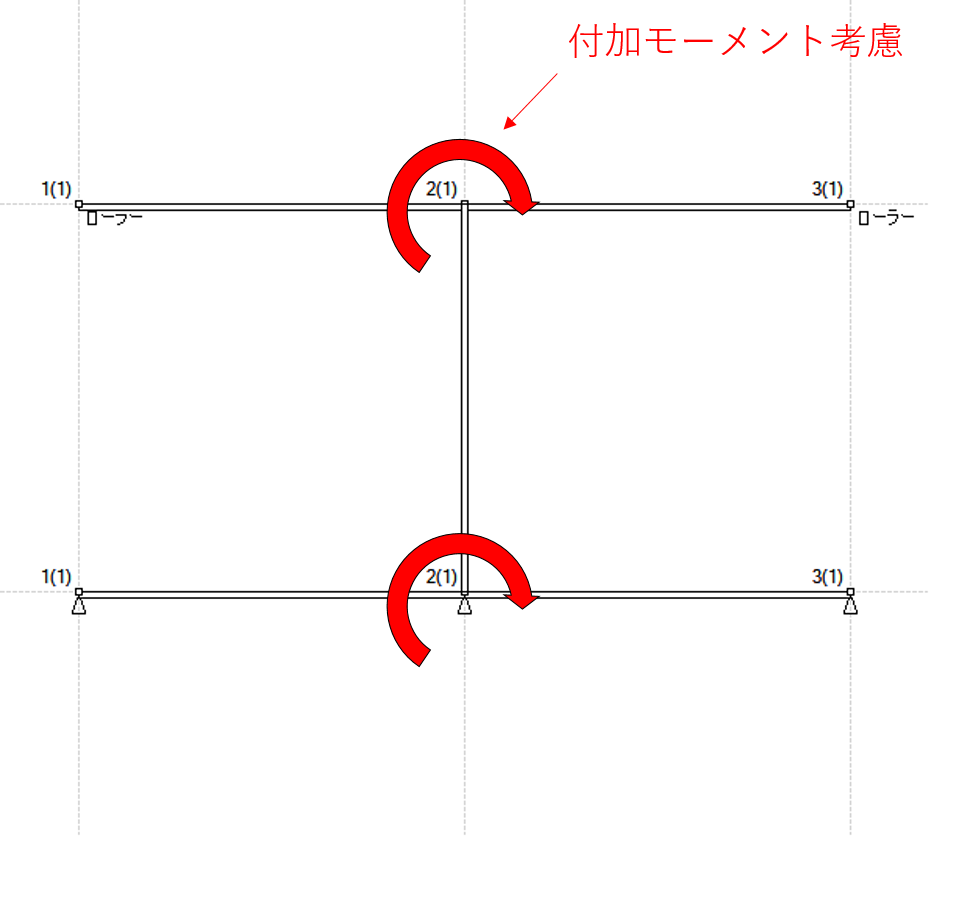
付加モーメント考慮

幾何剛性考慮
以下では、①P-Δ効果を考慮しない場合、②外力として作用させた場合、③幾何剛性として考慮した場合 の3ケースの結果を示します。
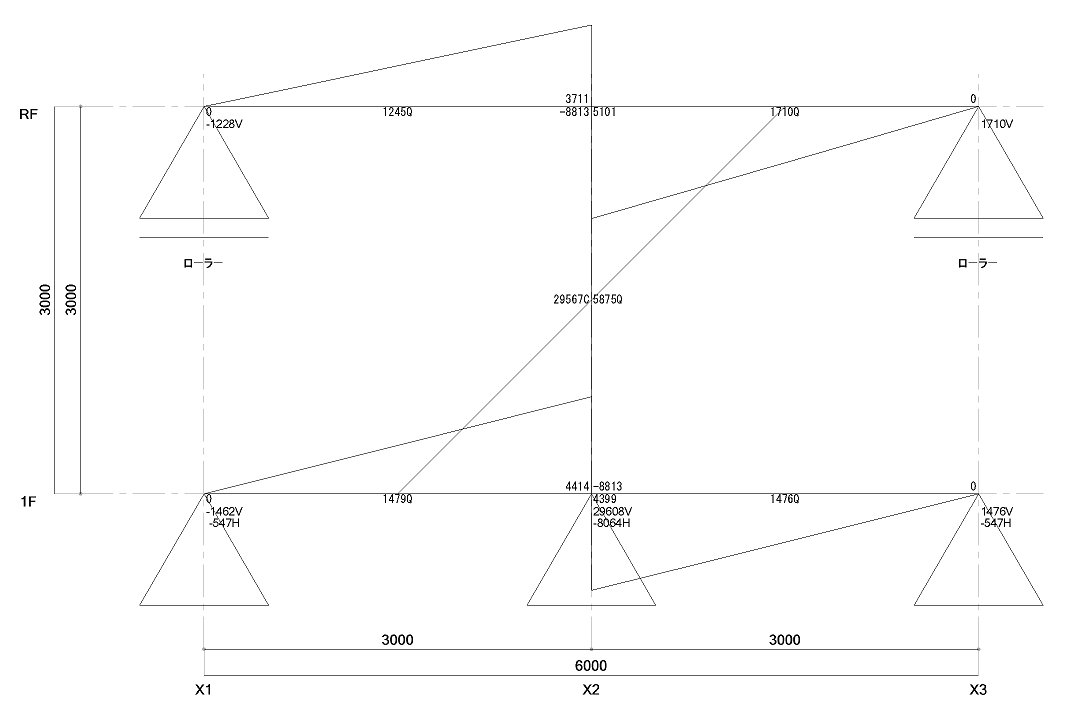
解析結果 : ①P-Δ効果を考慮しない場合
まずはP-Δ効果を考慮しない場合の結果を示します。これが基本の結果になります。
解析結果 : ②外力として作用させた場合
外力として作用させた場合の結果を示します。
付加モーメントは、各ケースの水平変形がおおむね100mm程度であったため、100mm変形時のモーメントが最終ステップで作用するように外力を増分しました。
外力として作用させた場合、以下のようなことが生じます。
- 節点周りでモーメントが0にならない
- 大梁のモーメントは2割程度増加
- 柱の応力は変化しない

解析結果 : ③幾何剛性として考慮した場合
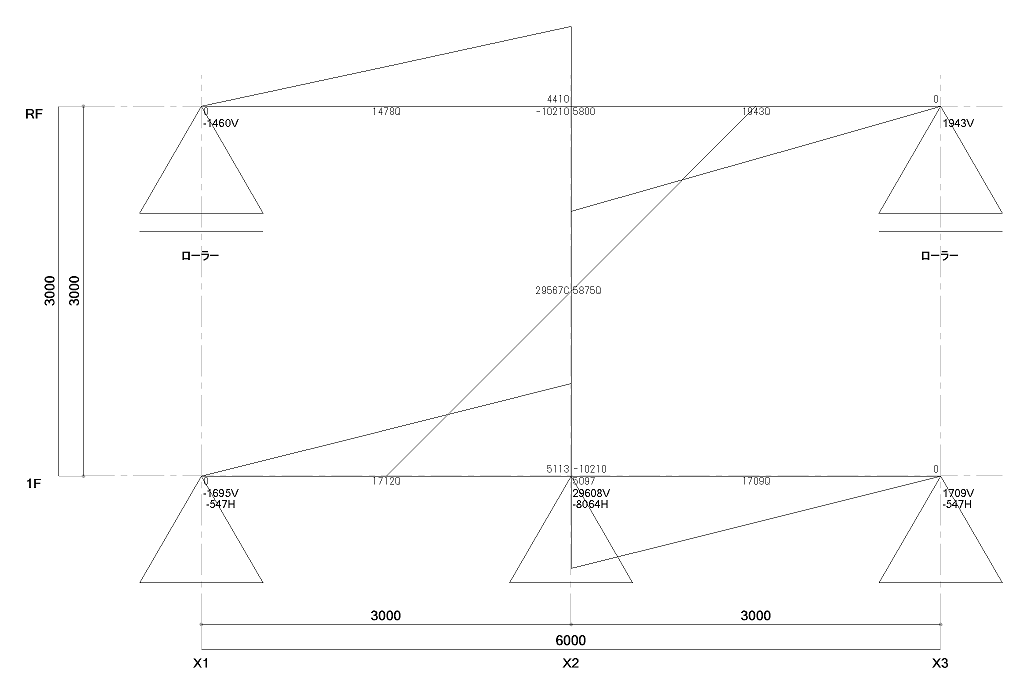
幾何剛性として作用させた場合の結果を示します。
幾何剛性として考慮した場合、以下のようなことが生じます。
- 大梁のモーメントは外力で考慮した場合とほぼ同等
- 柱のモーメントは増える
- 水平外力とせん断力は一致するが、柱のモーメント勾配がせん断力とならない
柱のモーメントは大きく増加していることから、外力として考慮する方法は周辺部材の応力は概ね適切に評価できますが、当該柱部材のモーメントについては過小評価しているということがわかります。水平荷重時の柱応力を評価する目的では、外力としてP-Δ効果を評価するのは適切ではないといえます。
柱のモーメント勾配がせん断力と一致しないのは、表示している値は幾何剛性による応力が含まれた値であるためです。材料剛性のみの応力であれば、モーメント勾配とせん断力は一致しますが、幾何剛性が圧縮軸力の場合には負剛性として作用することにより合算した応力ではせん断力が小さめに表現されます。この応力は外力と一致するせん断力となっています。
なお、現状ではプログラム上このような出力となっていますが、設計用応力は材料剛性のみによる応力を用いることが望ましいと思われます。今後出力を変更する可能性がありますが、現状ではモーメント勾配から求めたせん断力を設計用応力に用いていただければ、材料剛性のみによる応力となります。
各ケースの水平変形比較
各ケースの水平変位を比較します。
層間変形角 1/30rad を超える変形の場合、幾何剛性としてP-Δ効果を考慮すると最大17%程度変形が大きくなることが確認できました。
外力で考慮した場合と幾何剛性で考慮した場合の差異は、外力で考慮する際の変形を100mmと仮定しており、実際に幾何剛性考慮で生じた変形よりも1割程度小さいことも原因のひとつと考えられます。
| ①P-Δ考慮なし | ②外力で考慮 | ③幾何剛性で考慮 | |
| 水平変位(mm) | 96.1 | 105.9 | 112.6 |
| 層間変形角(rad) | 1 / 31 | 1 / 28 | 1 / 27 |
| 考慮なしに対する比率 | 100.0% | 110.1% | 117.1% |
まとめ
以下のようなことがわかりました。
- 外力で考慮する方法、幾何剛性で考慮する方法それぞれで周辺部材の応力についてはほぼ同等の結果が得られる
- 当該柱に生じるモーメントは、外力で考慮する方法では付加モーメントが評価されない
上記を踏まえ、目的ごとに使い分けていただけますと幸いです。
2019/10/29 追記
わかりにくい、という声をいただきましたので一部追記いたします。
おそらく、幾何学的非線形性を当然のように用いる構造物をよく扱っていらっしゃる技術者の方に対して、主にビル物の建築構造物におけるP-Δ効果の限定的な取り扱いが理解しづらい、という側面があるのではと考え、補足いたしました。
ビル物の建築構造物は基本的に微小変形理論で設計され大変形的な計算は必要とされませんが、変形が大きくなる場合には、P-Δ効果により周辺部材の応力が無視できない程度増加することが懸念されます。その影響を比較的簡便に評価する方法ということで今回の手法をご紹介しています。最後変形の話でまとめてしまっているため趣旨が伝わりにくくなってしまったものと思われますが、どちらかといえば応力の評価が設計としては重要な観点になると思います。
超高層ビルにおいても多くの場合はP-Δ効果の影響は十分小さい、で特別な検討が不要な場合が多いですが、RESPユーザー様の主要な対象構造物のひとつである大規模な鉄骨超高層建物の設計に用いたい、というユーザー様のニーズで機能追加した経緯があります。
貴重なご意見ありがとうございました。
今回使用したソフト RESP-D
採用情報
構造計画研究所 RESPチームでは、いっしょに働いていただけるエンジニアを募集しています。
構造設計・構造解析だけでなく、プログラミング技術を活かして新しいものを生み出したいと思っている方、ぜひご応募ください。
採用HPはこちら→https://www.kke.co.jp/recruit/