柱梁の曲げ非線形挙動を表現するために、広く一般的に用いられるものとして材端剛塑性ばねモデルというものがあります。
このモデルは、部材に生じる塑性ヒンジを材端の回転ばねで表現しようとするものです。部材が弾性の領域では、材端ばねを剛(剛性が無限大)と仮定し、塑性ヒンジが発生する段階で、初めて材端回転ばねを有効にします。
モデルのイメージはこんな感じです。
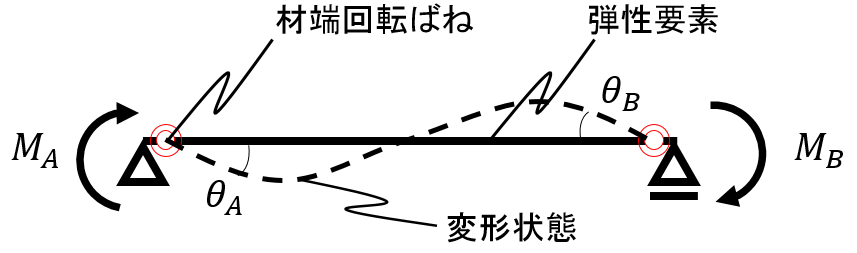
このとき、曲げモーメントMと材端回転角θの関係(曲げ復元力特性)は以下のようになります。
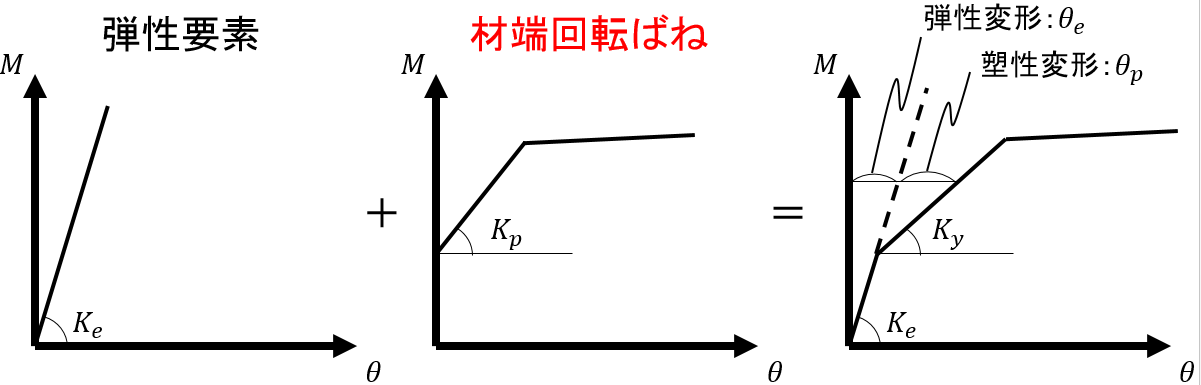
一般的に、何かしらの構造計算プログラムを利用する場合は、ユーザが材端回転ばねの剛性Kpを入力することはありませんから、これはプログラム側が計算していることになります。ユーザが定義した曲げ復元力特性になるように、材端回転ばねの剛性Kpを計算するのです。そのためには上図に示したように、初期剛性Keと初期剛性に対する剛性低下率α(あるいは降伏後剛性Ky)が必要になりますが、剛性低下率αはユーザが指定するため、あとは初期剛性Keさえ与えられれば材端回転ばねの剛性Kpが計算できます。
ここでひとつ疑問が湧きます。弾性範囲において、材端回転ばねが剛であるなら、そのときの初期剛性Keとは何なのでしょうか。これは、あくまでも材端回転ばねの剛性Kpを計算するための基準となる剛性にすぎません(弾性範囲では決して使われることのない剛性です)。実際に部材がどのような変形をしてどのような応力分布になるか分からない状態で、復元力特性を予め決めようとするのですから、何かしらの仮定・基準が必要になるのです(実際には、部材の曲げ剛性は曲率分布、つまりは曲げモーメント分布により異なる※)。
※同じ曲げモーメントMが作用していても部材に渡って生じている曲率Φが異なれば回転角θが異なるためM-θ関係は異なる=剛性が異なる
この材端回転ばねの剛性Kpを計算するための基準となる剛性Keは、一般的には、逆対称曲げモーメント分布を仮定して6EI/Lとします。これはプログラムにより変更できたりできなかったりしますが、片持ち梁であれば曲げモーメント分布は逆対称ではなくなります。このときは3EI/Lが適切と言えます。この仮定した剛性に基づき、材端回転ばねの剛性Kpを計算します。これで、材端剛塑性ばねモデルの出来上がりです。
が、、、先ほど仮定した6EI/L(逆対称曲げモーメント)がやや気になります。一般的なラーメン架構においては成立しやすい仮定ですが、そうでない場合には、成立しないかもしれない仮定です。
そこで少し検証してみました。
例えば以下のような逆対称曲げモーメントが生じる一本のRC梁部材を周辺部材の取り付き等の理由からモデル化上、2本に分割したとします(以下、分割モデルと呼ぶ)。分割モデルは要素を分割してしまったがために、逆対称曲げモーメントがそれぞれの梁に仮定されるため、一本の梁としては仮定が成立しないものになります。
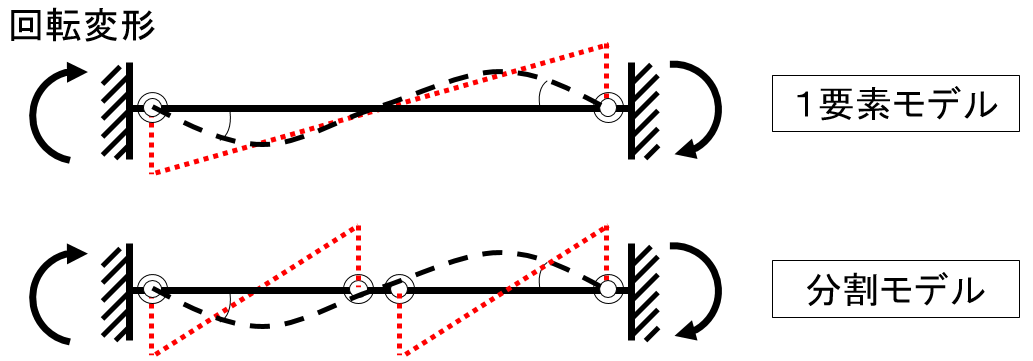
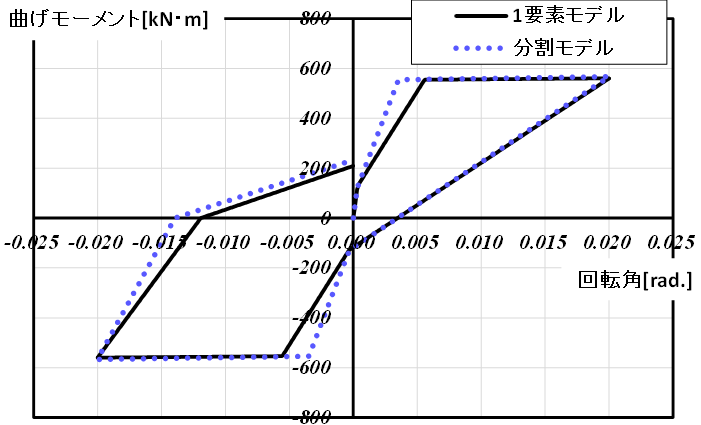
この場合の節点の曲げモーメントと回転角の関係を描いてみると、仮定が成り立つ場合(1要素モデル)と成り立たない場合(分割モデル)で以下のような差が生じます。
立体骨組みモデルを作成していると、上述したように、モデル化上仕方なく一本の大梁を分割せざるを得ない状況に出くわすことがあるかもしれませんが、その際に、一般的な構造計算プログラムではここで示したように、材端回転ばねモデルの仮定が成り立たなくなること、さらには解析結果に影響を及ぼす可能性があることをモデル化を行う際に認識しておくことが大変重要であると言える結果になりました。
以上をふまえて・・・
本モデルの注意点としては以下が挙げられます。
・実際の応力状態が予め仮定した曲げモーメント分布と異なる場合には、解析精度に影響を及ぼす
一方、利点としては以下が挙げられます。
・材端に塑性域の変形を集中させることでモデル化および評価が明快になる
・計算が簡単になる
・材端回転ばねに様々な履歴モデルを適用できる
・弾性範囲では単純な梁要素であり、理論解が得られる(マルチスプリングモデルでは、応力状態が仮定と異なる場合、弾性範囲から解析精度に影響を及ぼしてしまう)
今回は材端剛塑性ばねモデルの概要・特徴について整理してみました。
