シアリンク型ダンパーを質点系モデルに組み込む
ユーザー様からのお問い合わせで、シアリンク型ダンパーを質点系モデルに組み込む場合に考えるべきことを教えてほしい、という旨のお問い合わせをいただきました。
シアリンク型ダンパーは通常のブレースダンパーと異なり、ダンパーが取り付く節点が直接柱梁接合部に接続していません。
これが質点系モデル化に対してどのような影響を及ぼすか、試しに解析を行ってみました。
なお、シアリンク型ダンパーについては「RESP-Dならできる50のこと」の以下の記事もご参照ください。
【50のこと】シアリンク型オイルダンパーを配置したい
解析してみる
モデル概要
今回は以下のようなシンプルなモデルを対象にしました。
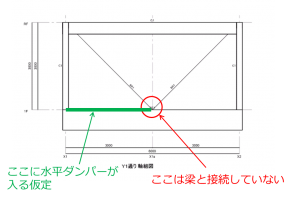
鉛直変位がないと仮定した場合
まず、ブレースの柱梁接合部側の節点が上下方向に移動しないと仮定すると、ブレース部分の水平剛性はブレース角度から簡単に算出することができます。
今回検討したモデルは以下のような諸元となっています。
ブレース剛性 EA : 5.355✕108 Nm
ブレース材長 L : 4.243 m
したがって、ブレースの水平剛性成分は、
ブレースばね剛性をK、水平剛性(2本分)をK'とすると、
K = EA / L = 1.262✕108 N/m
cosθ = cos(45°) = 1 / √2
K' = K✕(cos2θ)✕2 = 1.262✕108 N/m
となります。
鉛直変位があると仮定した場合
一方、鉛直変位を考慮した場合、単純な手計算で影響を評価することは難しくなります。この場合、「パッシブ制振構造設計・施工マニュアル」による状態N,状態Rの方法により付加剛性を算出する事が考えられます。
状態NとはNo-Damper, 状態RとはRigid-Damperを示しており、それぞれダンパー剛性を0、無限大と考えたモデルです。
状態Nではダンパー剛性がないことにより直列している付加ばね剛性が効かず実質的に架構のばね剛性のみとなります。状態Rではダンパー剛性が無限大のため架構と付加ばねの並列剛性となります。したがって、状態Rの剛性から状態Nの剛性を差し引くと付加ばねの剛性が残る、という考え方です。

状態Rとして、中間節点を水平拘束したモデル、状態Nとして中間節点を完全にフリーに
したモデルを作成しました。
各モデルにおける水平力は共通で P = 100 kN (1.0✕105 N) としています。
状態Rでは層間変位δR=0.81mm(8.1✕10-4 m), 状態Nでは層間変位δN=9.97mm(9.97✕10-3 m)となりました。
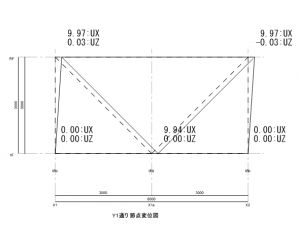
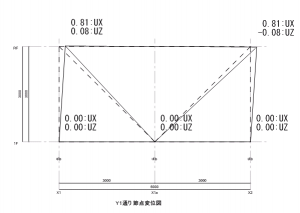
左 : 状態N, 右 : 状態R
したがって、各モデルの層剛性は
KR = 1.0✕105 / 8.1✕10-4 = 1.23✕108
KN = 1.0✕105 / 9.97✕10-3 = 1.01✕107
よって、付加剛性は以下となります。
K' = KR - KN = 1.129✕108 N/m
結果として、鉛直変位を考慮しない概算と比較して、約1割小さい付加剛性となりました。
まとめ
以下にまとめます。
- 鉛直変位を考慮しない概算、鉛直変位を考慮した方法(状態N,状態Rによる解析)により付加剛性を比較した。
- 今回検討を行ったシンプルなモデルにおいては、鉛直変位がない場合の概算に対して鉛直変位を考慮した方法では約1割小さい付加剛性となった。
今回のシンプルなモデルにおいては、概算による付加剛性でも設計上は十分に有用な精度を有していそうです。
ただし、今回は非常にシンプルなモデルであり、実設計レベルのモデルで同様の傾向となるか、あるいはどういった場合に影響が大きくなるかというところは気になるところです。今後、より複雑な条件の立体モデルでも検討を行ってみたいと思います。