本記事は2017年度建築学会大会梗概 「免震建物にレーリー減衰を適用する場合の留意点」の内容を再編集したものです。
著者:鈴木 壮, 梁川幸盛, 宇佐美祐人, 木村まどか
KeyWord:免震構造, 質量比例減衰, 剛性比例減衰, レーリー減衰
1. はじめに
建築構造物の減衰評価においては質量マトリクスや剛性マトリクスに比例させて減衰マトリクスを作成する比例減衰1)がよく用いられる。建築構造物においては剛性マトリクスのみに比例させる剛性比例減衰が慣例的によく採用されるが、その場合減衰定数を設定する固有周期よりも短周期の応答に対する減衰が大きくなる傾向がある。したがって、1 次モードに対して減衰定数を定めた場合、より高次モードの減衰が過大評価となる可能性がある。そのため、より高次の応答についても減衰を小さく設定したい場合には質量比例項も用い、レーリー減衰1)を採用することもある。
例えば、免震建物において水平動と上下動の同時入力による地震応答解析を行いたい場合には水平方向の固有周期と上下方向の固有周期に対してそれぞれ一定の減衰定数を与えるようなレーリー減衰を与えるということはよく行われる。
レーリー減衰は質量比例減衰と剛性比例減衰を組み合わせたもので、2つの固有周期に対して減衰定数を定めることができる特徴を持つ。しかしながら、減衰定数が同じだとしても質量比例項と剛性比例項ではマトリクスの形状が異なる。前者は対角マトリクスであるのに対し、 後者は非対角マトリクスとなる。したがって、図1に示すように前者は相対速度に対するダッシュポットとして作用するのに対し、後者は層間速度に対するダッシュポットとして作用することになる。これは、免震構造のように相対変位と層間変位で10倍以上の差が発生しうる場合には大きな影響となることが考えられる。
本稿では、この減衰マトリクス形状が異なることにより免震建物の応答がどのような影響を受けるかについて検討を行い、剛性比例減衰と同程度の応答を与えるレーリー減衰の設定方法について提案を行う。
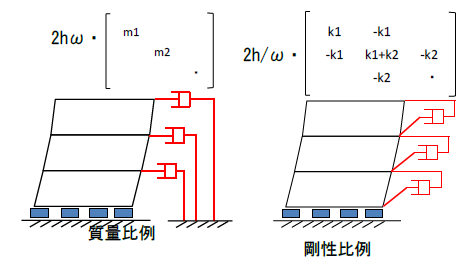 図1 各減衰における仮定
図1 各減衰における仮定2. 2質点モデルによるパラメトリックスタディ
質量比例減衰と剛性比例減衰の応答性状の差異を確認するため、2質点系モデルによるパラメトリックスタディを行う。1層目が免震層、2層目が上部構造を仮定する。1層目の剛性k1は免震の固有周期Tisoを4秒と仮定し、以下の式から算出した。
$$k_1=\frac{(m_1+m_2)×(2π)^2}{T_{iso}}, T_{iso}=4.0$$
2層目の剛性k2は、上部構造のみの固有周期TbがTb=1.0, 2.0となる値となるよう、以下の式から算出した。
$$k_2=\frac{m_2×(2π)^2}{T_b}, T_{b}=1.0, 2.0$$
各諸元を表1に示す。減衰の設定方法を図2に示す。上部構造の減衰設定方法としては以下の 3 つのケースで計算を行った。
(1)上部構造固有周期Tbに対する剛性比例減衰
(2)上部構造固有周期Tbに対する質量比例減衰
(3)免震固有周期Tisoに対する質量比例減衰
免震層の減衰設定方法は各ケース共通で免震層の剛性に対する 10%の剛性比例減衰とした。入力地震動は告示波乱数位相の基盤波を入力した。解析には(株)構造計画研究所の「3次元フレーム汎用解析プログラム RESP-F3T」を用いた。
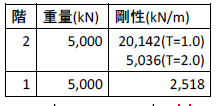
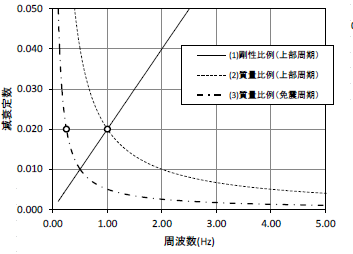 図2 各減衰の設定方法(2 質点)
図2 各減衰の設定方法(2 質点)各ケースの比較を表2に、層の最大応答結果を図3に示す。表2に示した通り、 (2)質量比例(上部周期)が全体的に応答を過小評価するのに対し、(3)質量比例(免震周期)では免震層変位以外はほぼ(1)剛性比例減衰と一致する。免震層変位のみ5%程度下回るため、直接免震層変位を評価する場合には注意が必要である。減衰力の時刻歴を図4に示す。結果より、いずれのケースも(2)では(1)よりも著しく減衰力が大きくなっている。
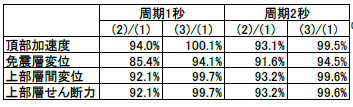
 図3 2質点モデル層の最大応答値(左:上部周期1秒, 右:上部周期2秒)
図3 2質点モデル層の最大応答値(左:上部周期1秒, 右:上部周期2秒)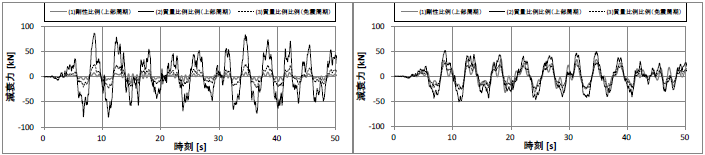 図4 減衰力時刻歴の比較(左:上部周期1秒, 右:上部周期2秒)
図4 減衰力時刻歴の比較(左:上部周期1秒, 右:上部周期2秒)Tb=1.0, 2.0 では Tb=1.0 の方が減衰力の差が大きくなっている。Tb=1.0 のケースで(1)と(3)を比較した場合、減衰力としては 2倍以上の差が生じているものの、上部構造層間変位、層せん断力はそれほど差が生じなかった。この原因としては、(1)、(3)における上部構造の減衰が免震層の減衰に対して十分小さいためであると考えられる。通常の免震構造であれば多くのエネルギー吸収は免震層で生じるため、今回の結果のように質量比例型、剛性比例型のマトリクス形状による違いが上部構造に与える影響は小さいと考えられる。一方で(2)では免震層変位、上部構造応答が(1)に比べて最大15%程度過小評価となっている。(2)のように基礎固定周期に対して質量比例減衰を適用した場合には免震層の減衰に対して過剰な減衰となっていることが考えられる。
3. 立体モデルによる検証
X方向3スパン、Y方向スパンのRC造基礎免震建物において以下の減衰を適用した解析(図5参照)を行い、結果を比較する。階数は10階、20階の2ケースとした。
(1) 初期剛性比例減衰(h=0.02)
(2) 上部構造周期に対する質量比例減衰(h=0.02)
(3) 免震周期と上部周期に対するレーリー減衰(h=0.02)
解析は立体弾塑性振動解析とした。立体モデルの諸元を表3に、固有周期を表4に示す。
層の最大応答値の比較を図6に示す。いずれのモデルにおいてもレーリー減衰は免震層変位においては剛性比例減衰よりも過小評価となるが、それ以外の応答についてはほぼ近い結果を示した。一方、層間変位は10階モデルではほぼ一致するのに対し、20 階モデルではレーリー減衰の方が大きい応答となった。これは、剛性比例減衰の方が高次モードに対する減衰が大きいため、高次成分の影響が大きい20階モデルで差が顕著になっていると考えられる。
 図5 各減衰の設定方法(立体)
図5 各減衰の設定方法(立体)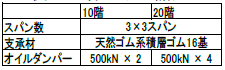
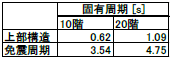
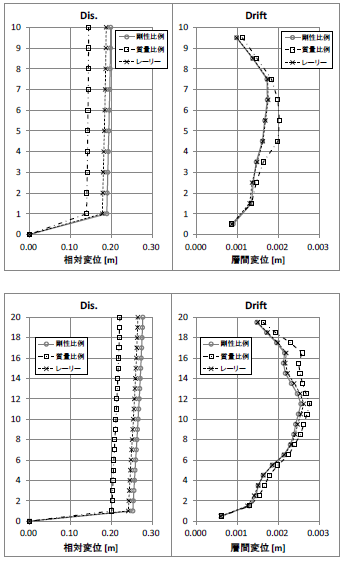 図6 層の最大応答値(立体, 上:10階モデル、下:20階モデル)
図6 層の最大応答値(立体, 上:10階モデル、下:20階モデル)4. まとめ
結果より、 以下のことがわかった。
・免震構造にレーリー減衰を適用する場合、減衰定数を設定する目標固有周期に上部構造周期ではなく免震周期を用いることが望ましい。
・レーリー減衰の長周期側の目標固有周期に免震等価周期を採用すれば、剛性比例減衰とほぼ同等の結果となる。ただし、免震層変位については過小評価する可能性があるため注意が必要である。
参考文献
1) 日本建築学会:建築物の減衰, 丸善株式会社, 2000.10