本記事は2019年度建築学会大会梗概 「既往の曲げ降伏時剛性低下率に適合する RC 部材のファイバーモデル化 その 2 立体骨組モデルによる確認」の内容を再編集したものです。
著者:角 友太郎, 鈴木 壮, 宇佐美 祐人, 木村 まどか
Keyword:ファイバーモデル, 材端剛塑性ばね, 塑性化領域, RC造, 立体骨組モデル
1. はじめに
その 1 では、付着すべりの影響を考慮するために鉄筋の復元力特性をトリリニアでモデル化することで構築したファイバーモデルについて、部材レベルでその有用性を検討した。本稿では、提案モデルの有用性について立体骨組モデルを用いて検討した結果を示す。
2. 検討方法
立体骨組モデルを 2 種類作成した。1 つは低軸力状態を想定した低層モデル、1 つは高軸力状態を想定した高層モデルである。表 1 にモデル諸元、図 1 にモデル図を示す。1 階柱でヒンジが発生しやすくなるように、ピロティ形式として 2 階以上は耐震壁を配置している。
この立体骨組モデルの柱部材に、軸力変動を考慮した材端剛塑性ばねモデル ¹⁾(以下、M-Theta)と本研究で考案したファイバーモデル ²⁾(以下、Fiber-Tri)をそれぞれ適用して、Ai分布による荷重増分解析により、柱部材のモデル化による結果の差異を比較することで、提案モデルの有用性を検討する。検討した柱部材のモデル化について整理したものを表 2 に示す。
Fiber-Triの検討にあたっては、塑性化領域長さ(以下、Lp)をパラメータに加えており、本検討では 0.5D と 1.0D について検討した。各階剛床仮定として、梁は材端剛塑性ばねモデルとする。柱梁共にせん断によるひび割れ及び降伏は考慮しないこととする。解析プログラムは株式会社構造計画研究所開発・販売の「RESP-D」及び「RESP-F3」を用いる。
表 1 立体骨組モデル諸元


図 1 立体骨組モデル図
表 1 柱部材モデル化

3. 検討結果
荷重増分解析により得られた 1 階の層せん断力-層間変形角関係を図 2,3 に示す。ここで、層間変形角は重心位置としており、いずれのモデルにおいても 1 階の柱頭、柱脚に曲げヒンジが発生して、柱の曲げ耐力で層のせん断耐力が決定する結果となっている。
ひび割れから降伏までの区間(M-Theta の二次勾配部分)において、付着すべりを考慮せず鉄筋をバイリニアでモデル化するファイバーモデルではLpにも依るが、M-Theta に比べて剛性を高く評価する傾向にある一方で、Fiber-Triは鉄筋の復元力特性をトリリニアでモデル化したことより剛性が低下して、M-Thetaと比較的良い一致を示している。また、Lp=1.0D の場合、Lp=0.5D の場合に比べて各部材の塑性化領域が大きいため、これに伴い層復元力特性上も比較的剛性低下が大きくなることが分かる。これらの傾向は低層モデルと高層モデルで共通である。
なお、層のせん断耐力については、Fiber-Triにおいて概ね最大耐力が発揮される 1/75 の層間変形角においてM-Thetaとの差異は最大で 1 割程度である。この差異は、M-Thetaが曲げ耐力をACI規準に基づいて等価応力度ブロック法を用いて算出している一方で、Fiber-Triは断面解析的に曲げ耐力を算出していることによるものと考えられる。また、Fiber-Triではコンクリートの復元力特性 ³⁾において、本来の下降域を初期剛性の 1/1000 剛性として耐力低下させない設定としていることもこの要因のひとつである。

図 2 1階層せん断力-層間変形角関係(低層モデル)
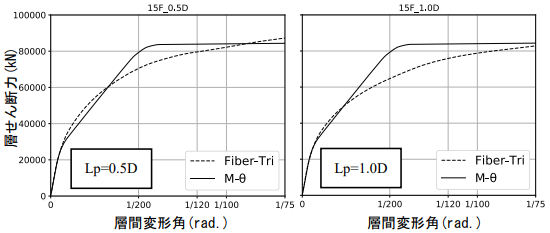
図 3 1階層せん断力-層間変形角関係(高層モデル)
層間変形角ごとの層(1 階)の履歴エネルギーについて、M-Thetaとの比率を算出したものを表 3 及び図 4 に示す。1/200、1/120、1/100 、1/75 のいずれの層間変形角においてもM-Thetaと概ね近い結果となっており、最大で 1 割程度の差異であった。Lpが本検討と同条件である場合、前述した通り、鉄筋をバイリニアでモデル化したファイバーモデルではM-Thetaの二次勾配の領域で剛性を高く評価する傾向があるため、これに伴いエネルギーを大きめに評価する傾向があるが、Fiber-Tri ではそのような傾向が見られない結果となった。
表 3 層履歴エネルギー比


図 4 層履歴エネルギー比(左:低層モデル,右:高層モデル)
部材曲げ塑性率基点について、M-Thetaとの比率を算出したものを表 4 及び図 5 に示す。1 階の引張側柱(X1,Y1)と圧縮側柱(X5,Y1)について、柱脚の曲げ塑性率を算出して比較した。なお、Fiber-Triについては重み付け平均法 ⁴⁾を用いて算出している。ケースによってMThetaよりも大きく評価するか小さく評価するか異なり、差異は最大で 3 割程度であった。
表 4 部材塑性率基点比

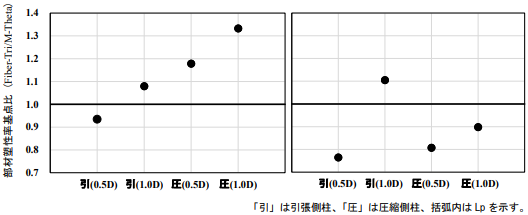
図 5 部材塑性率基点比(左:低層モデル,右:高層モデル)
4. 今後の課題
Fiber-Triは層復元力特性や層履歴エネルギーの観点からM-Thetaと比較的良い一致を示したが、塑性率基点の観点においては検討の余地がある。また、適切なLpの定方法や軸力との関係、繰り返し載荷時の性状の整理が望まれる。
5. まとめ
付着すべりの影響を考慮するために鉄筋の復元力特性をトリリニアでモデル化することで構築したファイバーモデルが、既往の曲げ降伏時剛性低下率を適用した材端剛塑性ばねモデルとの適合の観点において有用な可能性があることを示した。
参考文献
1) RESP-F3利用者マニュアル
2) 鈴木壮, 梁川幸盛ほか:材端剛塑性ばねモデルと適合するRC部材のファイバーモデル化に関する検討, 日本建築学会学術講演梗概集, 2016
3) 建設省総合技術開発プロジェクト:鉄筋コンクリート造の軽量化・超高層技術の開発, 平成 4 年度NewRC研究開発概要報告書, 国土開発技術センター, 1993
4) 鈴木壮, 會田裕昌ほか:ファイバー要素断面の塑性率算定に関する考察, 日本建築学会学術講演梗概集, 2013
関連ブログ
【構造解析TIPS】既往の曲げ降伏時剛性低下率に適合する RC 部材のファイバーモデル化 その1 両端固定梁要素によるパラメトリックスタディ