以前紹介した若林モデルについて、修正若林モデルや安定座屈耐力との応答性状の違いなどについて検証したいと思います。
比較用のモデル概要
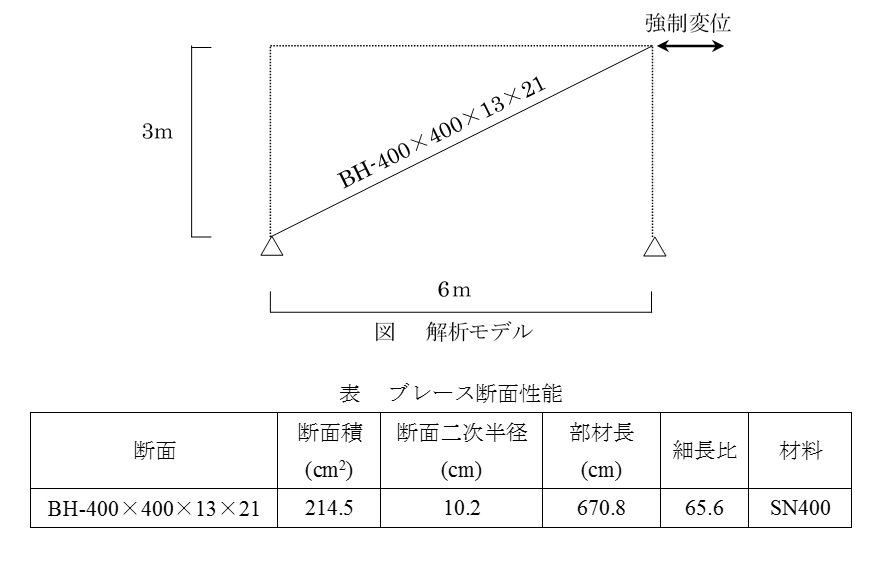
比較用の解析モデルは、図に示すブレースのみをモデル化したものを用います。このとき、ブレースは高さ3mスパン6mのフレームに配置することを想定した形状とします。表にブレースの断面性能を示します。今回検証に用いるブレースの復元力特性は若林モデルと修正若林モデル、安定座屈耐力に設定した標準型バイリニアの復元力特性を用います。
解析は変位増分解析を用い、強制変位をブレースの上部に作用させます。このとき、載荷条件は単調載荷(圧縮方向)と交番繰返し載荷の2ケースを検討します。
単純圧縮
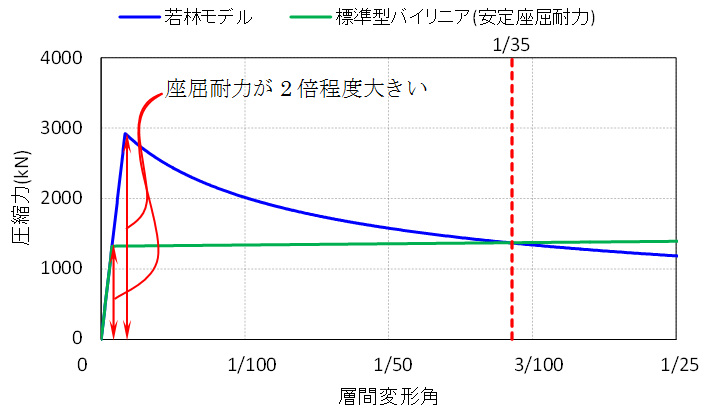
ブレースに圧縮力のみ載荷した場合の復元力特性の比較を行います。図に復元力特性の比較を示します。一度だけ圧縮力を載荷した場合、若林モデルと修正若林モデルの復元力特性は同じになるため、本節では修正若林モデルは割愛します。
復元力特性を見ると、ある変形までは若林モデルが標準型バイリニアよりも大きくなり、その後逆転するという形になっています。
圧縮降伏耐力は、若林モデルが安定座屈耐力の2倍程度あることが確認できます。そのため、動的解析ではブレースが座屈耐力まで達しないことがあるため、安定座屈耐力で座屈と判定していたブレースが、若林モデルを設定することで座屈しなくなる可能性があります。
交番載荷
ブレースに圧縮力と引張力を繰返し載荷した場合の復元力特性の比較を行います。このとき、ブレースに圧縮力と引張力を交互に3回ずつ載荷するように強制変位を与えます。強制変位量は層間変形角が1/200、1/100、1/50となるようにし、繰返すごとに大きな強制変位を掛ける解析とします。図に復元力特性の比較、図にエネルギーと載荷回数の関係図を示します。なお、軸力の符号は圧縮力を正としています。また、エネルギーは履歴面積から計算しています。

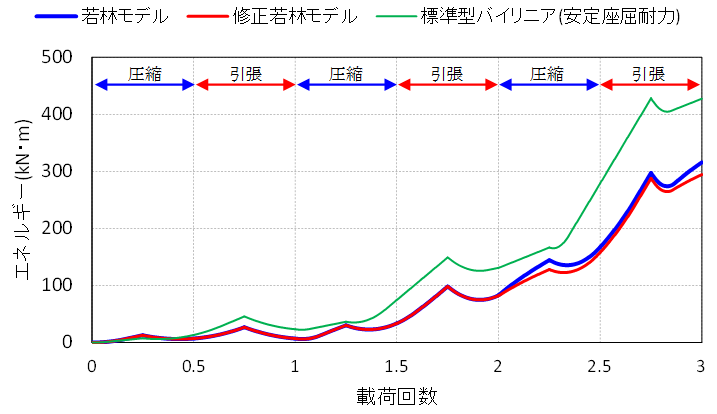
エネルギーと載荷回数の関係図を見ると、若林モデルに比べ標準型バイリニアのエネルギーが大きく、ひずみが大きくなるほどその差が大きくなる傾向にあります。安定座屈耐力の方が若林モデル(ないしは一般的な座屈耐力)よりも耐力が低いので安全側の設計になると思いがちですが、履歴面積を見ると安定座屈耐力の方が大きく評価されるという傾向があります。繰り返し載荷数の増加に伴ってより顕著になります。
これは圧縮側から引張側へ転じるときの履歴ループの部分で安定座屈耐力のほうが履歴面積が大きく評価されているからです。ただ、実現象を考えると座屈中のものが引張に転じる時、まずは歪んだ部分を元に戻す状態になるので初期剛性ですぐに引張側に転じるというのは過大評価であるといえます。
若林モデルと修正若林モデルの復元力特性を比較すると、累積圧縮ひずみが増えるにつれて座屈耐力の劣化による差が大きくなり、修正若林モデルの方が小さい座屈耐力になっています。また、エネルギーについても同様に耐力劣化の影響が見られる載荷回数が2~3回の部分から徐々に若林モデルと修正若林モデルで違いが生じています。
まとめ
若林モデル、修正若林モデル、標準バイリニア(安定座屈耐力)について解析しました。
座屈するまでの挙動と、履歴面積を正しく評価できることから動的解析では修正若林モデルを使うのが望ましいと思われます。
静的解析では若林モデルは負剛性を有するモデルであるため、解析が発散しやすいこと、荷重増分解析では最終的な変形を考えることが多いことから標準バイリニアモデルを使う方が無難であると言えます。
また、ブレースの座屈破断については日本建築学会から刊行されている「鋼構造物の座屈に関する諸問題2013」で触れられておりますので興味のある方はご覧ください。